2.3. Плоскость и прямая в пространстве

2.3.1. Пирамида SABC задана вершинами: S (2; 4; 6), A (3; -4; -2), S (-4; 3; -4), C (-4; -2; -6):

а) уравнение плоскости ASC ищем в виде:

где вектор n = {E, F, G} — нормальный вектор к плоскости ASC.

Его мы найдем из векторного произведения n = ABxAC. Прежде всего находим координаты векторов

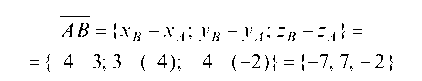
и

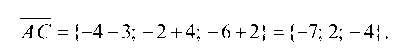
Тогда

= -24 • i-14 j + 35 • к.

Следовательно, n = {-24; -14; 35}. Подставляем в уравнение плоскости

или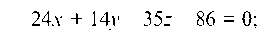

б) угол в радианах между ребром SC и гранью ASC найдем как угол между вектором CS = {2+4; 4+2; 6 + 6} = {6; 6; 12} и плоскостью ASC по формуле

Отсюда 0 = 16°59 ' 52" = 0,297 радиан (с точностью до 0,001);

127

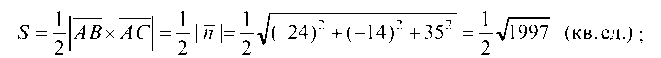
г) уравнение высоты SK, опущенной из точки S на грань ASC, ищем в виде:

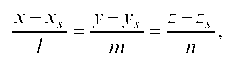
где вектор P{/; m; n} имеет такие же координаты как и вектор n = {-24; -14; 35}, так как эти векторы коллинеарны.

Тогда:

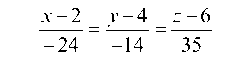
есть уравнение высоты SK.

Для определения длины высоты SK запишем нормальное уравнение плоскости ASC

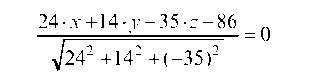
или

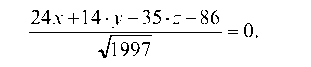
Тогда длина высоты SK определяется как

д) объем пирамиды SABC определяем с помощью смешанного произведения векторов:

Найдем тогда

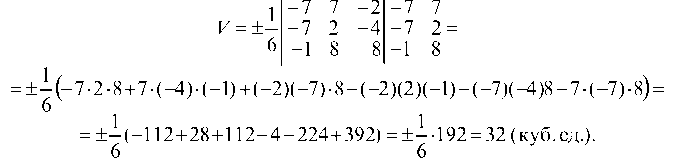
< Предыдущая		Следующая >