2.3. Исследование функций
Функция называется возрастающей (убывающей) в некотором интервале, если в этом интервале каждому большему значению аргумента соответствует большее (меньшее) значение функции. Как возрастающие, так и убывающие функции называются монотонными. Если функция не является монотонной, то область ее определения можно разбить на конечное число интервалов монотонности (которые иногда чередуются с интервалами постоянства функции).
Пример 2.25. Найти y ' (0) в точке А(1; 0), если еу + ху = е. Дифференцируем заданное соотношение и определяем y :
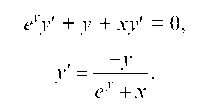
В последнее соотношение подставляем координаты точки А
х = 0, у = 1:
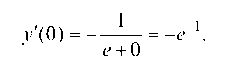
Монотонность функции y = /(х) характеризуется знаком ее первой производной / (х), а именно, если в некотором интервале /' (х) > 0 (/ (х) < 0), то функция возрастает (убывает) в этом интервале. Следовательно, отыскание интервалов монотонности функции y = /(х) сводится к нахождению интервалов знакопостоян-ства ее первой производной /'(х).
Отсюда получаем правило нахождения интервалов монотонности функции:
1. Найти нули и точки разрыва /' (х).
2. Определить методом проб знак /' (х) в интервалах, на которые полученные в п. 1 точки делят область определения функции /(х); интервалы, в которых / (х) > 0, являются интервалами возрастания функции, а интервалы, в которых / (х) < 0, — интервалами убывания функции. При этом, если на двух соседних интервалах, граничная точка которых является нулем производной/' (х), знак / (х) одинаков, то они составляют единый интервал монотонности.
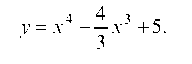
Решение. Область определения данной функции — вся числовая ось. Дифференцируя, находим

Точек разрыва производная y' не имеет. Нулями производной y' будут корни уравнения х2^ - 1) = 0, т. е. x1 = 0 и
x2 = 1.
Область определения функции — ось Ох — разбивается полученными точками на три интервала (-<»; 0), (0; 1), (1; +<»), в каждом их которых y' сохраняет определенный знак. Подставляя в
' 5 1 5
выражение для y значения x = -5, x = 7, x = 5 из этих интервалов,
получим соответственно знаки «-», «-», «+». Следовательно, в интервале (-<»; 1) функция убывает, а в интервале (1; +¥) — возрастает.
Точка x = х0 называется точкой максимума (минимума) функции у = f(x), если существует такая окрестность точки х0, что для всех х (х ф х0) этой окрестности выполняется неравенство

Точки максимума и минимума функции называются точками ее экстремума, а значение функции в точке максимума (минимума) — максимумом (минимумом) или экстремумом функции.
Точками экстремума могут служить только критические точки I рода, т. е. точки, принадлежащие области определения функции, в которых первая производная f'(x) обращается в нуль или терпит разрыв.
Точками экстремума являются лишь те из критических точек, при переходе через которые первая производная f'(x) меняет знак, а именно, если при переходе через критическую точку x = х0 в положительном направлении знак f'(x) меняется с «+» на «-» (с «-» на «+»), то точка x = х0 есть точка максимума (минимума).
Отсюда получаем правило отыскания экстремумов функции у = /(х):
1. Найти нули и точки разрыва / '(х).
2. Определить методом проб знак / (х) в интервалах, на которые полученные в п. 1 точки делят область определения функции /(х).
3. Из этих точек выделить те, в которых функция /(х) определена и по разные стороны от каждой из которых производная / (х) имеет разные знаки — это и есть экстремальные точки. При этом экстремальная точка х = х0 является точкой максимума, если при движения по оси Ох в положительном направлении она отделяет интервал, в котором производная / (х) > 0, от интервала, в котором / (х0) < 0, и точкой минимума — в противном случае.
В заключение заметим, что точки, в которых производная обращается в нуль, иногда проще исследовать на экстремум, выяснив знак второй производной / "(х0): точка х = х0, в которой /' (х0) = 0, а /"(х) существует и отлична от нуля, является экстремальной, а именно, точкой максимума, если /"(х0) < 0, и точкой минимума, если /"(х0) > 0.
Пример 2.27. Найти экстремумы функции y = х3^( х-1)2.
Решение. Функция определена на всей числовой оси. Вычислим производную:
, „ 2 3Г ГГ 3 2 х2 „ , . х2(11х - 9)
y = 3х У(х-1) + х • 3,-= 3,-(9х - 9 + 2х) =- - .
3 V х-1 3 V х-1 3 V х-1
9
Производная /' обращается в нуль при х = 0 и х = — и не существует при х = 1. Полученные точки разбивают числовую ось
| на четыре интервала, | в каждом из которых / сохраняет опреде- | ||
| ленный знак: (-да, 0), | (0,11 (^ | ]> (1, +¥). | Найдем знак произ- |
| водной у в полученных интервалах: | |||
| в интервале | (-¥, 0) | имеем | /' (-1) > 0; |
| » » | (0-SI | » | y 11 )¦ * |
| » » | (H-iI | » | ¦1^ S )¦ • |
| »» | (1, +¥) | » | у' (5) > 0. |
Экстремальными являются точки x1 = — — точка максимума и х2 = 1 — точка минимума. Экстремумы функции получим, вычислив ее значения в экстремальных точках:
максимум и у(1) = 0 — минимум
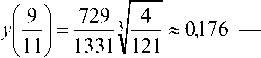
функции.
Кривая называется выпуклой (вогнутой) в некотором интервале, если она расположена ниже (выше) касательной, проведенной к кривой в любой точке этого интервала. Выпуклость или вогнутость кривой, являющейся графиком функции у = f(x), характеризуется знаком второй производнойf"(x), а именно, если в некотором интервале f"(x) < 0 f"(x) > 0], то кривая выпукла (вогнута) в этом интервале.
Таким образом, отыскание интервалов выпуклости и вогнутости графика функции у = f(x) сводится к нахождению интервалов знакопостоянства ее второй производной f"(x).
Точкой перегиба кривой называется такая ее точка, которая отделяет участок выпуклости от участки вогнутости.
Точками перегиба графика функции у = f(x) могут служить только точки, абсциссы которых являются критическими точками II рода, т. е. точки, находящиеся внутри области определения функции у = f(x), в которых вторая производная f"(x) обращается в нуль или терпит разрыв.
Точками перегиба графика функции у = f(x) являются лишь только те из указанных точек, при переходе через которые вторая производная f"(x) меняет знак.
Отсюда получаем правило отыскания интервалов выпуклости и вогнутости и точек перегиба графика функции:
1. Найти точки, в которых вторая производная f "(x) обращается в нуль или терпит разрыв.
2. Определить методом проб знакf "(x) в интервалах, на которые полученные в п. 1 точки делят область определения f(x); интервалы, в которых f"(x) < 0, являются интервалами выпуклости, а интервалы, в которых/"(x) > 0, — интервалами вогнутости графика функции у = f(x). При этом если на двух соседних интервалах, граничная точка которых является нулем второй производной f"(x), знак f "(x) одинаков, то они составляют единый интервал выпуклости или вогнутости.
3. Из полученных в п. 1 точек выделить те, в которых функция f(x) определена и по разные стороны от каждой из которых вторая производная f"(x) имеет противоположные знаки — это и есть абсциссы точек перегиба графика функции у = f(x).
Пример 2.28. Найти интервалы выпуклости и вогнутости и точки перегиба графика функции f(x) = 3х5 + 5х4 - 20х3 + 60х - 5.
Решение. Функция определена на всей числовой оси. Дифференцируя ее дважды, получим
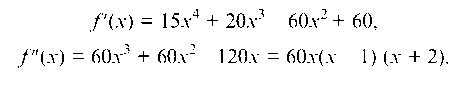
Вторая производная существует на всей числовой оси и обращается в нуль при х = -2, х = 0 и х = 1. Этими точками область определения разбивается на четыре интервала (-да, -2), (-2, 0), (0, 1), (1, +да), в каждом из которых f"(x) сохраняет знак. Определяя знак второй производной в произвольно взятой точке каждого из интервалов, получим знак ее в соответствующем интервале:
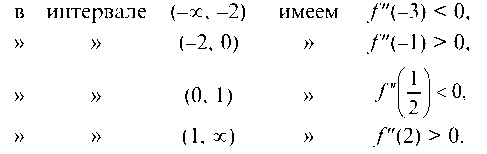
Таким образом, в интервалах (-да, -2) и (0, 1) кривая выпукла, а в интервалах (-2, 0) и (1, да) — вогнута.
Граничные точки х1 = -2, х2 = 0, х3 = 1 этих интервалов являются абсциссами точек перегиба. Вычислим значения функции у = f(x) в этих точках:
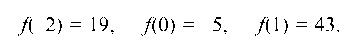
Итак, данная функция имеет три точки перегиба: (-2; 19), (0; -5), (1; 43).
Ассимптотой кривой называется прямая, к которой неограниченно приближается точка кривой при ее удалении по кривой в бесконечность.

I. Если, то прямая х = а есть асимптота кривой у = /(х). Например, кривая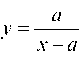 Имеет асимптоту х = а.
Имеет асимптоту х = а.
II. Если в правой части уравнения кривой у = /(х) можно выделить линейную часть у = /(х) = кх + b + а(х) так, что оставшаяся часть а(х) ® 0, когда х ® ±¥, то прямая у = кх + b есть асимптота кривой.
Примеры:
1) криваяимеет асимптоту у = х + 1 (и асимптоту х = 0);
2) кривая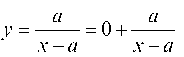 Имеет асимптоту у = 0.
Имеет асимптоту у = 0.
III. Если существуют конечные пределы И
И
 То прямая у = кх + b есть асимптота.
То прямая у = кх + b есть асимптота.
Для отыскания наибольшего и наименьшего значений функции, непрерывной на некотором отрезке [a, b], надо вычислить значения этой функции на концах отрезка и во всех ее критических точках, принадлежащих этому отрезку (такими точками в данном случае являются точки, в которых первая производная функции обращается в нуль или не существует). Наибольшее и наименьшее из полученных значений являются соответственно наибольшим и наименьшим значением функции на отрезке.
В случае, если исследуемая функция претерпевает разрыв в некоторых точках отрезка [a, b] или же задана на бесконечном интервале, то необходимо дополнительно рассмотреть ее поведение в окрестности точек разрыва и при х ® ±¥.
Пример 2.29. Найти наибольшее и наименьшее значения следующих функций:
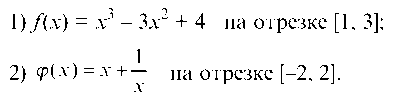
97
Решение.
1. Функция f(x) непрерывна на отрезке [1, 3]. Находим

В данном случае критическими являются только точки, в которых производная f'(x) равна нулю, т. е. х = 0 и х = 2. Отрезку [1, 3] принадлежит лишь одна из этих критических точек, а именно х = 2. Вычислим значения функции f(x) в точке х = 2 и на концах отрезка х = 1 и х = 3:


Таким образом, наибольшее значение функции равно 4 и достигается на правой границе отрезка в точке х = 3; наименьшее значение функции равно нулю и достигается ею во внутренней точке х = 2.
2. Функция j(x) претерпевает разрыв в точке х = 0, принадлежащей отрезку [-2, 2]. Исследуем поведение функции в окрестности точки разрыва:
Следовательно, вблизи точки х = 0 функция j(x) достигает сколь угодно больших по абсолютной величине как положительных, так и отрицательных значений, и, следовательно, не имеет ни наименьшего, ни наибольшего значения.
Исследование функции рекомендуется проводить по следующей схеме:
1. Найти область определения функции, установить точки разрыва и интервалы непрерывности функции.
2. Исследовать функцию на четность, нечетность.
3. Найти, если это возможно, точки пересечения с осями координат. Вычислить предельные значения функции на границах области определения. Найти асимптоты кривой, если они существуют. После этого можно построить примерный вид графика, удовлетворяющего проведенному исследованию.
4. Уточнить характер графика с использованием первой производной, т. е. исследовать функцию на экстремум, установить интервалы монотонности функции.
5. Уточнить характер графика по второй производной, т. е. исследовать функцию на выпуклость, вогнутость, точки перегиба.
Пример 2.30. Построить график функции
Решение.
1. Функция определена и непрерывна на интервале (-<»; <»).
2. Функция нечетная, т. к. у(-х) = - у(х), т. е.
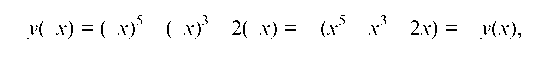
следовательно, график функции симметричен относительно начала координат, поэтому достаточно провести исследование для х > 0.
3. Найдем точки пересечения кривой с осями координат

Определим значения функции на границах области существования, т. е. при х ® ±¥.

Вертикальных асимптот нет, т. к. функция не имеет точек разрыва. Определим наклонные асимптоты y = кх + b.
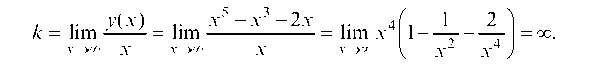
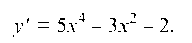
Найдем критические точки 1-го рода


х1 = -1; х2 = 1 — критические точки 1-го рода.
Чтобы выяснить, являются ли эти точки экстремальными, используем второе достаточное условие экстремума. Для этого определим знак второй производной в найденных критических точках:
Подставив значение х = 1 в y" (берем только один корень, т. к. проводим исследование для х > 0 в силу нечетности функции), получим y"(1) = 14 > 0; значит, в точке х = 1 функция достигает минимума (при х = -1 — максимума). Вычислим экстремальные значения функции:
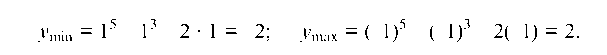
Составим таблицу изменения знаков первой производной.
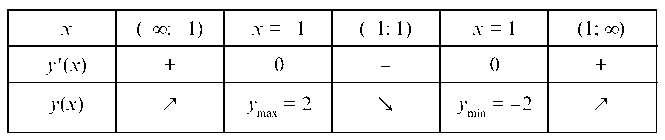
5. Найдем критические точки 2-го рода, приравняв к нулю правую часть y":
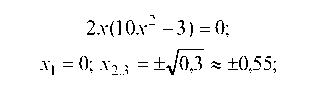
100
х1 = 0, х2 = -/0,3, х3 = Д3 являются критическими точками 2-го рода, которые делят всю числовую ось на интервалы:
(-¥; - д/03), (-Л/0,3; 0), (0^70,3), (^0,3; ¥). Выясним знак второй
производной в указанных интервалах. На интервале (-»; --^/0,3) возьмем, например, точку х = -1; y "(-1) = -14 < 0, значит, кривая в этом интервале выпукла.
На интервале (-0,3; 0) рассмотрим точку
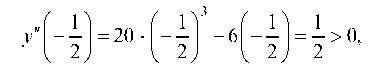
значит, кривая на этом интервале вогнута, вторая производная при переходе через х2 = ->/0з меняет знак с - на +, следовательно, значение х = -^/0,3 является абсциссой точки перегиба. Аналогично определяем, что на интервале (0^^/0,3) кривая выпукла, а на интервале (V03; ¥) — вогнута; значения х = 0 и х = являются абсциссами точек перегиба кривой.
Составим таблицу изменения знаков y "(х).
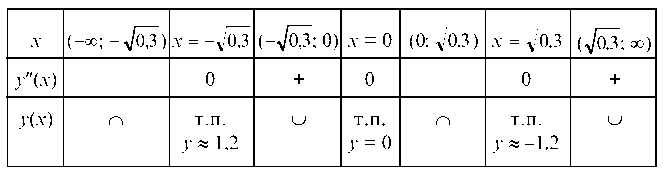
Определим значения функции в точках перегиба:
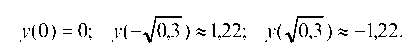
Чтобы точнее нарисовать кривую графика, можно найти углы наклона касательных, проведенных к кривой в точках перегиба. Так, при х = 0, у' (0) = -2, т. е. tga = -2, где a — угол наклона касательной к кривой в точке х = 0, а при х = д/0,3,
y'(V0,3)» -2,45. Окончательный график функции y = х5 - х3 - 2х изображен на рис. 24.
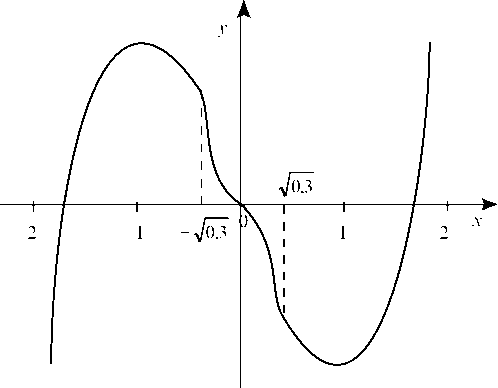
Рис. 24
Пример 2.31. Провести полное исследование и построить график функции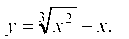
1. Функция определена всюду на интервале (-<»; <»).
2. Функция общего вида.
3. Найдем точки пересечения с осями координат:
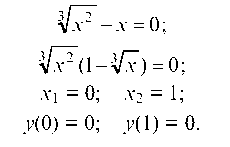
Определим значения функции на границах области существования:
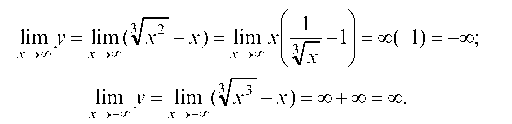
Вертикальных асимптот нет, так как функция не имеет точек разрыва. Определим наклонные асимптоты:
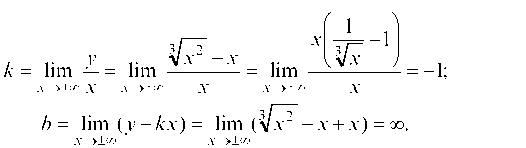
Так как b ® ¥ при х ® ¥, то наклонных асимптот кривая не имеет.
На рис. 25 изображена простейшая кривая, удовлетворяющая проведенному исследованию.
Рис. 25
4. Далее продолжим исследование по первой производной
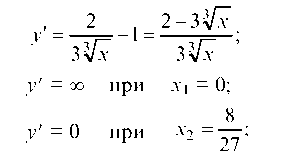
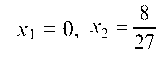
— критические точки.

Чтобы выяснить, являются ли они точками экстремумов, используем первое достаточное условие экстремума
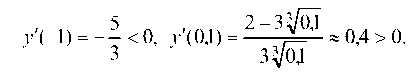
При прохождении через точку х1 = 0, у' меняет знак с « -» на «+»; значит, точка х = 0 является точкой минимума функции, причем функция имеет в этой точке так называемый острый эстремум:
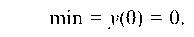
8
При прохождении через точку x2 = — мы аналогично можем проверить, что первая производная меняет знак с «+» на «-». Значит, точка x2 = 27 является точкой максимума:
Составим таблицу изменения знаков первой производной.
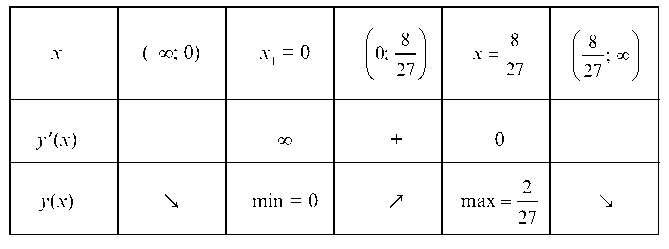
5. Найдем вторую производную.
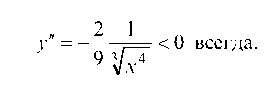

Вторая производная всегда отрицательна, значит, точек перегиба нет, кривая всегда выпукла. Окончательный график функции изображен на рис. 26.

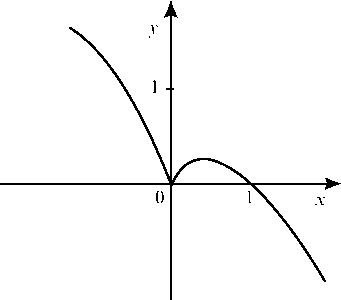
Рис. 26
Пример 2.32. Провести полное исследование и построить график функции
Областью определения функции являются интервалы (0; 1) ^ (1; ¥).
Функция Является функцией общего вида. При 0 < x < 1
Является функцией общего вида. При 0 < x < 1
y < 0, при 1 < x < ¥ y > 0.
Вычислим предельные значения функции на границах области существования:
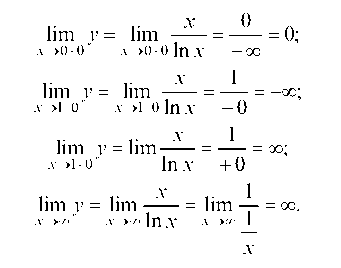
В последнем случае применено правило Лопиталя.
Из найденных пределов ясно, что прямая х = 1 является вертикальной асимптотой.
Определим наклонные асимптоты:

Наклонных асимптот функция не имеет, горизонтальных асимптот не имеет также. Примерный ход графика изображен на рис. 27.

Ищем экстремум функции. Ее производная: 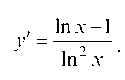 у '= 0 при x = e — критическая точка.
у '= 0 при x = e — критическая точка.
у' = ¥ при x = 1 — граничная точка, она не может быть экстремальной.
Итак, имеем одну критическую точку x = e.
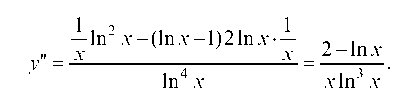
Чтобы проверить, является ли точка x = e экстремальной, найдем знак y" в точке x = e
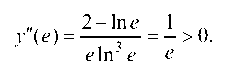
Значит, точка x = e является точкой минимума функции. Здесь мы использовали второе достаточное условие экстремума. Определим точки перегиба функции: y" = 0 при x = e2 — критическая точка 2-го рода; y" = ¥ при x = 1, но эта точка не является критической точкой 2-го рода, так как она является г2раничной точкой.
При прохождении через x = e y" меняет знак с + на -, так как

абсциссой точки перегиба,
значит, значение x = e2 является
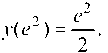
Составим таблицу изменения знаков первой и второй производных.

Окончательный график функции изображен на рис. 28.

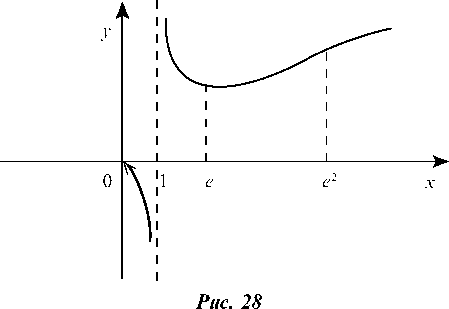
Пример 2.33. Исследовать и построить график функции
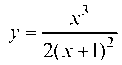
Функция существует всюду, кроме х = -1, т. е. ее областью определения являются интервалы (-¥; -1), (-1; ¥).
Найдем точки пересечения кривой с осями координат:

Определим значения функции на границах области существования:

Очевидно, прямая х = -1 является вертикальной асимптотой функции. Определим наклонные асимптоты:
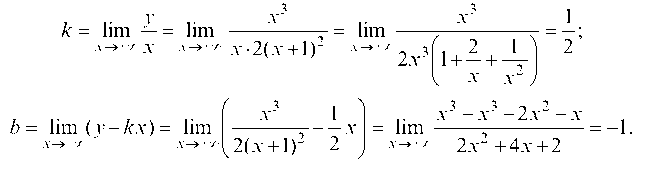
Итак, прямая Является наклонной асимптотой кривой, причем точки кривой
Является наклонной асимптотой кривой, причем точки кривой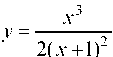 Будут неограниченно приближаться к прямой
Будут неограниченно приближаться к прямой Как при х ® -¥, так и при х ® ¥. 108
Как при х ® -¥, так и при х ® ¥. 108
На рис. 29 построена простейшая кривая, удовлетворяющая проведенному исследованию.
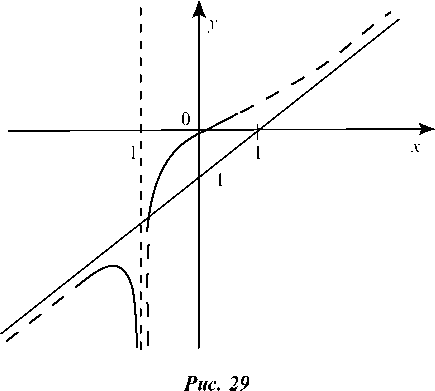
у' = 0 при х1 = -3 и х1 = 0 — критические точки 1-го рода. у' = ¥ при х = -1 — граничная точка.
Находим производные:

Проводя обычное исследование, находим, что при х = -3 функция достигает максимума , а в точке х = 0 экстремума нет, так как первая производная при прохождении через х = 0 знак не меняет.
, а в точке х = 0 экстремума нет, так как первая производная при прохождении через х = 0 знак не меняет.

Составим таблицу изменения знаков первой и второй производных.
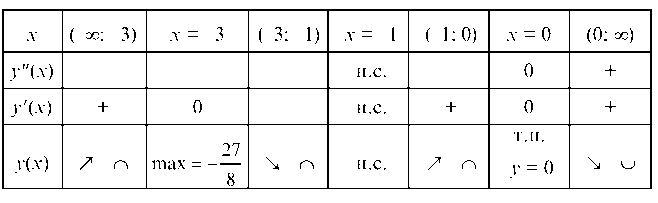
Находим, что х = 0 является абсциссой точки перегиба функции, причем у(0) = 0.
График является выпуклым на интервалах (-¥; -1) и (-1; 0) и вогнутым на интервале (0; ¥).
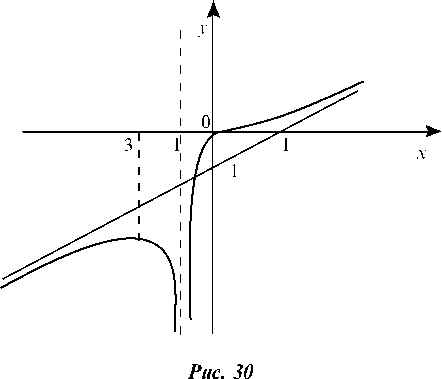
Окончательный график функцииизображен на
рис. 30.
| < Предыдущая | Следующая > |
|---|