2.2.4. Дифференцирование неявных функций

Определение. Если зависимость у от х задается посредством соотношения Дх, y) = 0, где Дх, y) — выражение, содержащее х и у, то у называется неявной функцией от х. Для определения производной от неявно заданной функции нужно обе части уравнения F(x, y) = 0 продифференцировать по x, рассматривая y как функцию от x, а затем из полученного равенства выразить y'.

Для определения y'' нужно аналогично уравнение F(x, y) = 0 дважды продифференцировать по х и исключить y'.

Пример 2.23. x4 - 6x2y3 + 15y2 - 100 = 0. Найти y'. Дифференцируем заданное соотношение, рассматривая при этом у как функцию от х

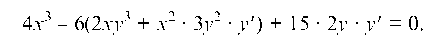
23

(здесь, при дифференцировании слагаемого 6x y использовано правило дифференцирования произведения).

Решаем полученное уравнение относительно y':

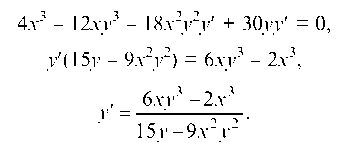
Пример 2.24. arc tg(x + y) = x. Найти y''.

Дифференцируем обе части заданного соотношения и определяем затем y':

откуда

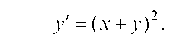
Находим далее y'':

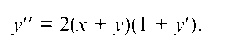
В правую часть последнего равенства подставляем вместо y' ее значение, найденное ранее:

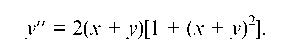
< Предыдущая		Следующая >