2.2.3. Производные высших порядков
Определение. Производной второго порядка (или второй производной) от функции y = f(x) называется производная от ее производной, т. е. y" = (y')'.
Обозначается вторая производная так:
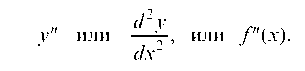
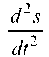
Если s = f (t) — закон прямолинейного движения точки, то
есть ускорение этого движения. Аналогично, производная третьего порядка функции y = f(x) есть производная от производной второго порядка y'" = (y")'.
Вообще, производной n-го порядка от функции y = f (x) называется производная от производной (n - 1)-го порядка:
Для n-ой производной употребляются обозначения:

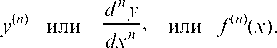
Производные высших порядков (вторая, третья и т. д.) вычисляются последовательным дифференцированием данной функции.
Пример 2.19. y = (arc tg x). Найти у".
Находим первую производную:

Вторая производная, по определению, равна производной от первой производной, следовательно:
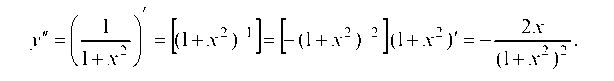
Пример 2.20. Найти y ' "(3), если / (х) = (2х - 3)5.
Находим последовательно первую, вторую и третью производные:
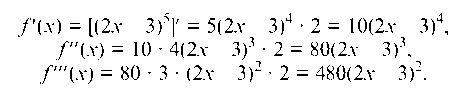
Подставляя в третью производную значение х = 3, получим:
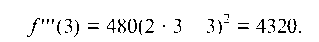
Пример 2.21. Найти y' '' ' от функции y = sin2x
Находим последовательно первую, вторую, третью и четвертую производные: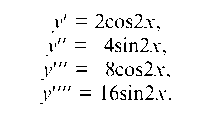
Пример 2.22. Показать, что функция y = е2х • sin5x удовлетворяет дифференциальному уравнению:
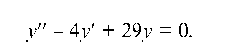
Найдем первую и вторую производные от функции y = е2х • $ш5х:
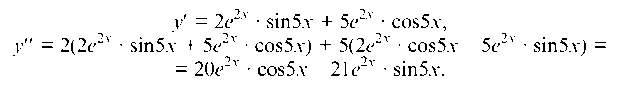
Подставим найденные выражения для y и y в данное уравнение и получим тождество:
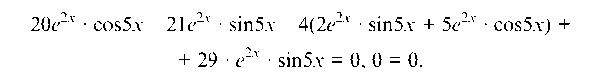
| < Предыдущая | Следующая > |
|---|