2.2.2. Механический смысл производной

Если при прямолинейном движении точки задан закон движения S = s(t), то скорость движения в момент ^ есть производная пути по времени:

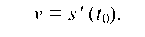
Пример 2.15. Какой угол образует с осью абсцисс касательная к кривой y = x3 + 4x, проведенная в точке М0 (1; 5). Написать уравнения касательной и нормали, проведенных к кривой в данной точке.

Для определения углового коэффициента касательной находим производную от заданной функции:

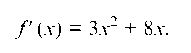
Далее определяем численное значение производной в точке M0 (1; 5), для этого подставляем в выражение производной х = 1:

Значение производной при х = 1 и дает искомый угловой коэффициент к = 11, т. е. tg а = 11, откуда а = arc tg (11) » 84°50'.

Для составления уравнения касательной используем формулу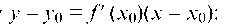

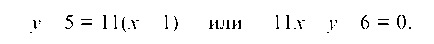
Для составления уравнения нормали пользуемся формулой

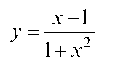
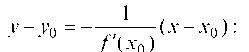
Пример 2.16. Определить, под каким углом кривая пересекает ось абсцисс.

Находим точку пересечения кривой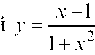- с осью OX, урав

нение которой у = 0, т. е. решаем систему:

откуда получаем х = 1.

Под углом данной кривой с осью OX понимается угол, который касательная к этой кривой в точке х = 1 образует с осью абсцисс. Найдем угловой коэффициент касательной к кривой в точке х = 1:

откуда

Пример 2.17. Под каким углом пересекаются параболы

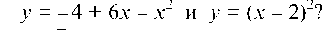
Решая совместно уравнения парабол, находим абсциссы их точек пересечения:

Определяем, что точки пересечения парабол, соответствующие найденным абсциссам — это точки Л(1; 1) и B(4; 4) (рис. 23).

Находим угловые коэффициенты касательных к параболам в точке А:

Вычисляем тангенс угла между касательными: откуда

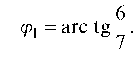
Также определяем угол между кривыми в точке 5:

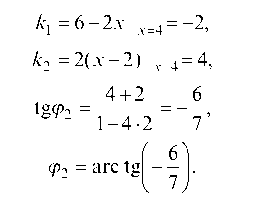
Пример 2.18. В какой точке параболы y = -^18х ордината возрастает вдвое быстрее, чем абсцисса?

Найдем производную от заданной функции:

Так как производная характеризует скорость возрастания ординаты (функции) по сравнению с возрастанием аргумента, то из условия задачи имеем:

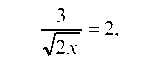
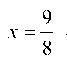
отсюда — абсцисса искомой точки.

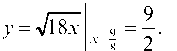
А ордината находится из уравнения Ответ:.

< Предыдущая		Следующая >