2.2.1. Основные правила дифференцирования
Пусть С постоянная, и(х), у(х) — дифференцируемые в точке х функции.
7. Если у = /(и), где и = и(х), (то есть у = /(и(х)) — сложная функция от х) и функции /(и) и и(х) дифференцируемы, то производная сложной функции у = /(и(х)) вычисляется по формуле


8. Если функция аргумента х задана параметрически
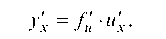

Определение. Дифференциалом функции у = /(х) называется главная часть ее приращения, линейная относительно приращения аргумента, то есть, если Dy = /'(х)Дх + а(Дх) ¦ Ах, где а (Ах) ® 0 — бесконечно малая функция при Дх ® 0, то дифференциал функции dy = /'(х)^х.
Дифференциал независимого аргумента равен приращению аргумента, то есть ^х = Дх. Следовательно, dy = /' (х) ¦ ^х.
Если Дх мало, то Dy » dy, и, следовательно, /(х + Дх) »/(х) + dy = =/(х) + /'(х)^х (формула приближенного вычисления с помощью дифференциала).
Пример 2.11. Найти производные данных функций:

б) применим теоремы о производной произведения и производной сложной функции:
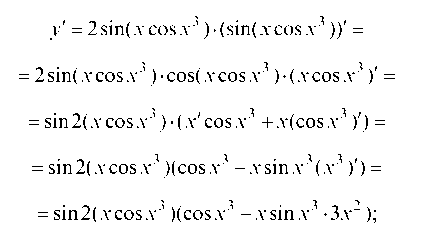
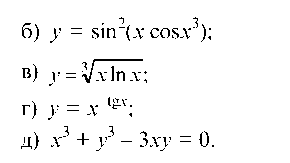
а) применим теорему о производной частного:
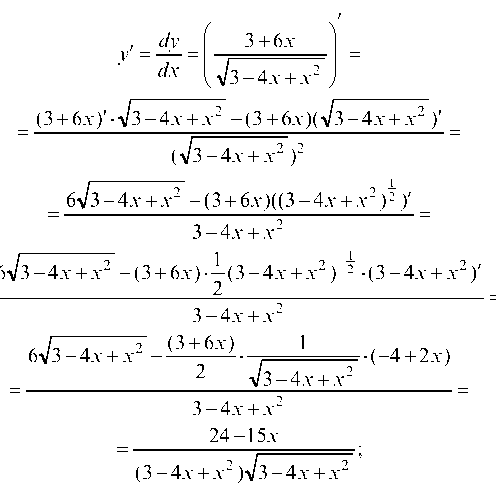
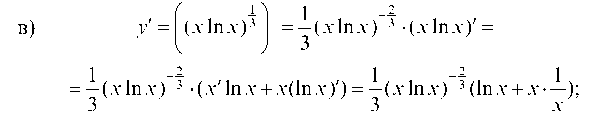
г) прологарифмируем обе части равенства:
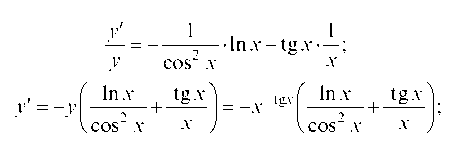
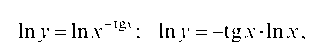
учитывая, что у является функцией от х, найдем производные обеих частей равенства: (In y)' = (-tg x • In x)'.
д) функция задана неявно. Для того, чтобы найти y', продифференцируем обе части равенства по х, считая у функцией от x(y = y(x)), а затем разрешим уравнение относительно y':

Пример 2.12. Найти производную функций:
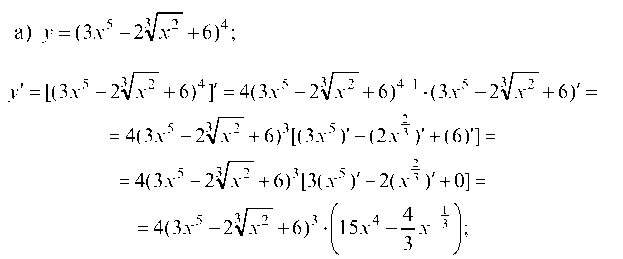

Пример 2.13. Найти производную функций:
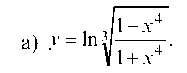
Используя свойства логарифмов, упростим

Находим производную
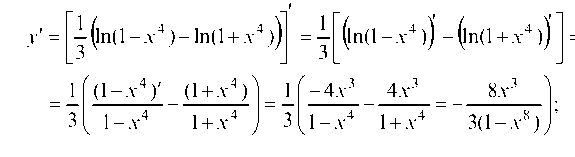
Преобразуем функцию

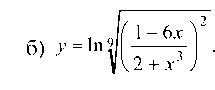
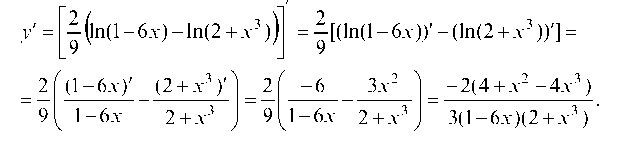
Пример 2.14. Найти производную функций: 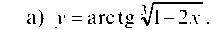 Дифференцируем
Дифференцируем

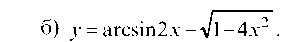
Дифференцируем

| < Предыдущая | Следующая > |
|---|