2.2. Производная и дифференциал
Пусть функция у = f(x) определена в некоторой окрестности точки х0 и y0 = f(x0). Если х получит некоторое положительное или отрицательное приращение Дх и примет значение х0 + Ах, то и функция у получит некоторое приращение Dy = Дх0 + Дх) - Дх0). Составим отношение приращения функции к приращению аргумента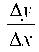 .
.
Определение. Функция y = f(x) называется дифференцируемой в точке х0, если существует

Этот предел называется производной функции y = f(x) в точке х0 и обозначается f '(x0) или .
.
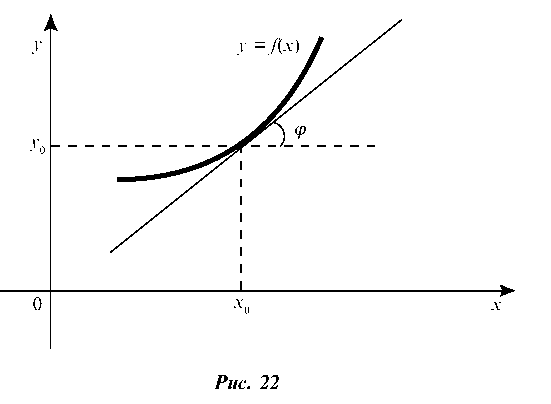
Геометрически производная представляет собой угловой коэффициент касательной к графику функции y = f(x) в точке x0, то есть y = tgj (рис. 22). Физически производная есть скорость изменения функции в точке x0.
| < Предыдущая | Следующая > |
|---|