2.2. Кривые второго порядка на плоскости

2.2.1. Составить уравнение линии, для каждой точки которой отношение расстояния до точки F (2; 4) к расстоянию до прямой / : х = -4 равно 2. Привести уравнение линии к каноническому виду и определить вид этой кривой.

Решение. Пусть M (х; у) — текущая точка линии. Из точки M опускаем перпендикуляр на прямую х = -4, которыйпересекается с ней в точке N (-4; у). По условию задачи:, или

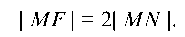
Тогда

или

Возводя в квадрат, раскрывая скобки и делая приведение подобных членов, получаем:

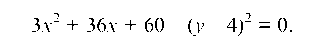
Коэффициент при х2 делаем равным единице, для чего все уравнение делим на 3:

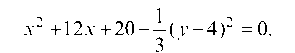
125

Многочлен, зависящий от х, записываем как полный квадрат: Тогда уравнение примет вид: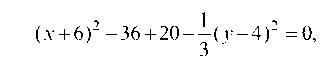

далее

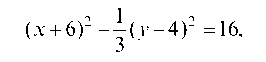
или, деля на 16, имеем:

Вводя новую систему координат:

приведем уравнение линии к каноническому виду:

Это есть каноническое уравнение гиперболы. m

Замечание. Если — = 1, то придем к каноническому уравнению n

параболы '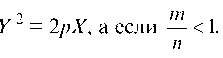То получим каноническое урав

нение эллипса:

< Предыдущая		Следующая >