2.1.1. Свойства непрерывных функций
1. Сумма и произведение конечного числа непрерывных функций есть функция непрерывная.
2. Частное от деления двух непрерывных функций есть функция непрерывная во всех точках, где делитель не равен 0.
3. Если и = <р(х) непрерывна в точке х = х0 и /(и) непрерывна в точке и = и0 = /(х0), то сложная функция /(ф(х)) непрерывна в точке х0.
4. Всякая элементарная функция непрерывна в каждой точке, в которой она определена.
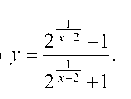
При x ф 2 функции, стоящие в числителе и знаменателе, непрерывны, и знаменатель не обращается в 0. Поэтому при х ф 2 функция Непрерывна. Исследуем точку х = 2. Найдем
Непрерывна. Исследуем точку х = 2. Найдем
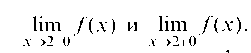
Так как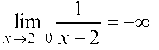 И, следовательно,
И, следовательно,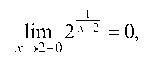 То
То
 . Далее, так как
. Далее, так как И, следователь
И, следователь
но,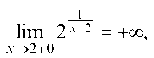 То преобразуем дробь
То преобразуем дробь
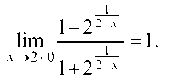
Таким образом,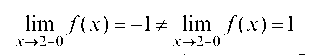 И, значит,
И, значит,
в точке х = 2 функция терпит разрыв 1-го рода. Скачок функции f(2 + 0) - f(2 - 0) = 1 - (-1) = 2.
Пример 2.9. Найти точки разрыва функции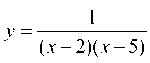 .
.
Очевидно, функция непрерывна при х ф 2 и х ф 5. Найдем пределы в указанных точках:
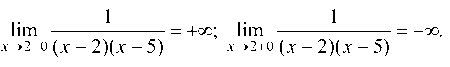
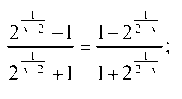
Следовательно, х = 2 — точка разрыва 2-го рода. 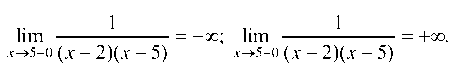 Следовательно, х = 5 — точка разрыва 2-го рода.
Следовательно, х = 5 — точка разрыва 2-го рода.

Поскольку созх, х + 1, х непрерывны всюду и, в частности на указанных интервалах, то функция /(х) непрерывна на интервалах (-—, 0), (0,1), (1, +—). Точками разрыва могут являться только точки х = 0 и х = 1. Исследуем эти точки на непрерывность:
/(0) = cos0 = 1.
Таким образом,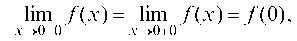 Следовательно,
Следовательно,
х = 0 — точка непрерывности функции /(х).

то есть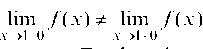 , следовательно, х = 1 — точка раз
, следовательно, х = 1 — точка раз
рыва 1-го рода. График функции

имеет вид (рис. 21).

| < Предыдущая | Следующая > |
|---|