2.1. Функции, предел, непрерывность
Одним из основных понятий математического анализа является понятие предела функции.
Определение. Число А называется пределом функции y = f(x) при x ® а, если для любого положительного сколь угодно малого числа e существует 5(e) > 0 такое, что при 0 < | x - а | < 5(e) выполняется неравенство | f(x) - A | < e. В этом случае пишут lim f (x) = A.
x®a При вычислении пределов функций используют следующие свойства пределов:

Для всех основных элементарных функций в любой точке их области определения имеет место равенство:

то есть предел функции находят непосредственный подстановкой предельного значения аргумента.
Пример 2.1.
Однако часто прежде, чем перейти к пределу, приходится проводить тождественные преобразования данного выражения.
Пример 2.2. Найти Здесь предел знаменателя равен нулю:
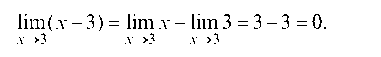
Следовательно, теорему о пределе частного применить нельзя. Но вблизи от точки хо = 3 имеем х - 3 ф 0 (при х ф 3), и поэтому дробь можно сократить на х - 3, т. е.

Последнее равенство имеет место при всех значениях х ф 3. Значит и

Но теперь можно применить теорему о пределе суммы, т. е. окончательно получаем
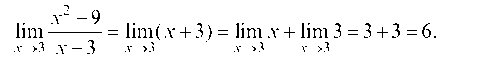

Соображения о возможности тождественных преобразований под знаком предела применимы не только в том случае, когда аргумент стремится к конечному пределу хо, но и при х ® ¥.
Пример 2.3. Найти lim 2x, + x.
x®¥ x3-1
В этом случае ни числитель, ни знаменатель не имеют предела, так как оба неограниченно возрастают.
Но если предварительно преобразовать аналитическое выражение под знаком предела, разделив числитель и знаменатель на x3, то получим:


Пример 2.4. Найти при: а) x0 = -1; б) x0 = 1,
в) x0 = ¥.
а) Подставляем в предел x = x0 = -1.

б) Как и в задаче 2.2 здесь предел знаменателя равен 0 при x ® 1, но в числителе и знаменателе можно выделить множитель (x - x0) = (x - 1) и тогда имеем:

Если вместо х подставить да, то имеем отношение двух бесконечно больших величин I — I. Тогда и числитель и знаменатель делим на х2:

Пример 2.5. Найти
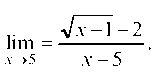
Здесь также имеет место неопределенность 0. Для разрешения неопределенности умножим числитель и знаменатель дроби на выражение, сопряженное числителю
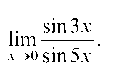

Пример 2.6. а) Найти Преобразуем заданное выражение:

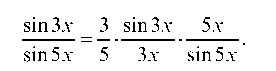
Обозначим и = 3х, заметим, что т. е. при
х ® 0 также и и ® 0, следовательно,


Следовательно,

в) Найти
Обозначим u = arctg 2x, тогда, очевидно tgu = 2x и при x ® 0 имеем u ® 0. Следовательно,

Пример 2.7. Найти
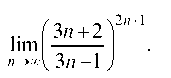
Преобразуем выражение в скобках:
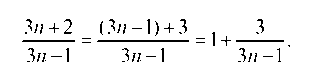


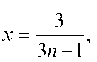
Обозначим теперь откуда и
причем, при n ® ¥ имеем x ® 0. Следовательно,
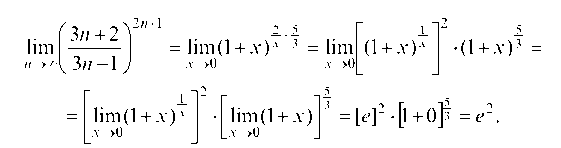
Определение. Функция у = /(х) называется непрерывной в точке х = хо, если она определена в некоторой окрестности точки х0 и выполняется равенство
Определение. Точка х = х0, принадлежащая области определения функции или являющаяся граничной для этой области, называется точкой разрыва, если в ней нарушается условие непрерывности.
Необходимым и достаточным условием непрерывности функции в точке является выполнение равенств:
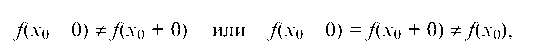

где /(х0 - 0) и /(х0 + 0) — односторонние пределы функции в точке х0 соответственно слева и справа.
Если эти равенства не выполняются или не существует хотя бы один из односторонних пределов, то точка х = х0 — точка разрыва функции, причем:
1) если существуют односторонние пределы, но
то точка х0 называется точкой разрыва 1-го рода;
2) если хотя бы один из пределов /(х0 - 0) или /(х0 + 0) не существует, то точка х = х0 называется точкой разрыва 2-го рода.
| < Предыдущая | Следующая > |
|---|