1.1.3. Метод исключения неизвестных (метод Гаусса)

Основная его идея состоит в том, что данная система линейных уравнений преобразуется в равносильную ей систему специального вида, где одно из уравнений системы содержит все неизвестные, второе — на одно неизвестное меньше, и т. д., последнее уравнение — лишь одно из неизвестных. Покажем это на примере.

Пример 1.5. Решить систему линейных уравнений методом Г аусса.

Решение. Примем за первое ведущее уравнение первое уравнение системы, а за первое ведущее неизвестное — X1; первым ведущим элементом будет ац = 2. Исключим X1 из второго и третьего уравнений, прибавив ко второму уравнению ведущее, умноженное на —, а к третьему — ведущее, умноженное на —. Получим:

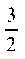
Первый шаг закончен. Второе и третье уравнения образуют первую подсистему. За второе ведущее уравнение примем второе уравнение системы, а за второе ведущее неизвестное — X2; вторым ведущим элементом будет. Исключим X2 из третьего уравнения. Получим:

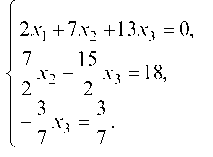
Второй шаг закончен. Вторая подсистема состоит из одного третьего уравнения. Прямой ход метода Гаусса закончен. Обратным ходом получаем:

Итак, решение данной системы будет: X1 = -4, х2 = 3, х3 = -1.

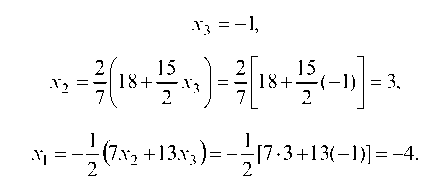
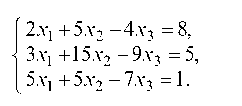
Уравнение 0 = -26 не имеет смысла, следовательно, данная система несовместна.

Решение. Преобразуем систему по методу Гаусса:

Замечание. Несовместность данной системы можно усмотреть уже после первого шага: в полученной системе левые части второго и третьего уравнений отличаются только знаком, тогда как правые части одинаковы по знаку и различны по модулю.

Пример 1.7. Решить систему линейных уравнений

Решение. Преобразуем систему по методу Гаусса:

После второго шага из трех уравнений осталось два, так как третье уравнение приняло вид 0 = 0 и удалено из системы. В данном случае ранг системы r = 2, а число неизвестных п = 3, т. е. r < п. Из трех уравнений исходной системы только два независимых (m = 3, r < m). В первой подсистеме два уравнения, вторая подсистема отсутствует. Прямой ход метода Гаусса закончен. Исключая теперь с помощью второго уравнения X2 из первого уравнения, приведем систему к виду

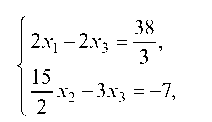
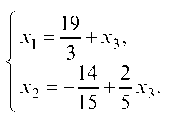
Неизвестные X1, X2 — базисные, X3 — свободное. Придавая неизвестному X3 произвольные числовые значения, можно получить множество частных решений:

откуда легко находим общее решение:

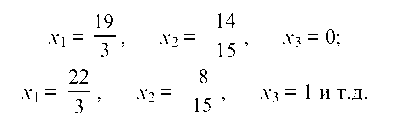
< Предыдущая		Следующая >