Вариант № 06

Исследовать числовой ряд на сходимость: .

Заметим, что при . Следовательно, 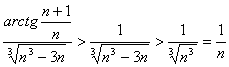. Но гармонический ряд расходится. Тогда расходится и данный ряд по первому признаку сравнения. Ответ: Ряд расходится.

Исследовать числовой ряд на сходимость: .

Заметим, что . Но ряд с общим членом сходится по признаку д, Аламбера: . Следовательно, исследуемый ряд так же сходится по первому признаку сравнения.

Ответ: Ряд сходится.

Исследовать числовой ряд на сходимость: .

Имеем . Функция удовлетворяет условиям интегрального признака Коши. Действительно, монотонно убывает на и, следовательно, интеграл и исходный ряд сходятся или расходятся одновременно. Имеем . Интеграл сходится, следовательно, сходится и данный ряд. Ответ: Ряд сходится.

Исследовать ряд на абсолютную или условную сходимость: .

Исследуемый ряд является знакочередующимся рядом: Он удовлетворяет всем условиям теоремы Лейбница. Действительно, по абсолютной величине члены ряда монотонно убывают, т. е. . Кроме того, при . Следовательно, ряд сходится. Рассмотрим ряд . Этот ряд расходится по признаку сравнения с гармоническим рядом , так как . Следовательно, исходный ряд сходится условно. Ответ: Ряд сходится условно.

5. Определить область сходимости функционального ряда: . Применим признак д, Аламбера к ряду :

. Ряд сходится, если этот предел будет меньше единицы: , т. е. . Или . Следовательно, интервал является интервалом сходимости данного ряда. Исследуем ряд на концах интервала. При получим знакочередующийся числовой ряд . Он расходится по признаку сравнения с гармоническим рядом. При получим такой же числовой ряд, только с положительным знаком, который расходится по тому же признаку.

Ответ: Областью сходимости ряда является множество

6. Определить область сходимости функционального ряда: .

Применим признак д, Аламбера к ряду 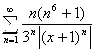: . Ряд сходится, если этот предел будет меньше единицы: , т. е. или . Следовательно, ряд сходится при и . Исследуем ряд на концах интервала. При получим знакочередующийся числовой ряд , который расходится, так как не выполняется необходимый признак сходимости. При получим числовой ряд , который расходится по той же причине.

Ответ: Областью сходимости ряда является множество .

Определить область сходимости функционального ряда: .

Это знакочередующийся ряд, так как . Поскольку всегда , то достаточно рассмотреть ряд . Применим признак д, Аламбера: . Ряд сходится, если этот предел будет меньше единицы: , т. е. . Следовательно, ряд сходится при . Исследуем ряд на концах интервала. При получим знакочередующийся ряд (здесь учтено, что ). Этот ряд сходится по признаку Лейбница. При получим числовой ряд , который расходится по признаку сравнения с расходящимся рядом . Действительно, . Ответ: Областью сходимости ряда является множество .

8. Разложить указанную функцию в ряд Тейлора по степеням . Указать область сходимости: .

Функция представляет сумму бесконечно убывающей геометрической прогрессии: , при условии , - знаменатель прогрессии. Преобразуем данную функцию: . Положим . Получим: . Этот ряд будет бесконечно убывающей прогрессией, если только , или . Очевидно, что на концах этого интервала ряд расходится. Следовательно, областью сходимости ряда будет область . Ответ: .

Указанную функцию разложить в ряд Маклорена, используя разложения в ряд функций указать область сходимости: .

Преобразуем данную функцию: . Воспользуемся разложением функции в ряд Маклорена:

. Этот ряд сходится при условии . В этот ряд подставим , получим: . Тогда . Областью сходимости ряда будет . Ответ: , .

10. Вычислить приближённо с точностью до 10-4: .

Воспользуемся формулой В данном случае вычисляется , т. е. . В соответствии с теоремой Лейбница заданная точность будет достигнута, если первое отбрасываемое слагаемое будет по абсолютной величине меньше, чем . В данном случае

. Слдовательно, достаточно взять два слагаемых: . Ответ:

11. Вычислить предел, используя разложение функций в ряд Тейлора: .

Так как , а , то . Ответ: .

12. Найти сумму ряда:.

Обозначим сумму ряда через S(X). Тогда . Но есть сумма бесконечно убывающей геометрической прогрессии при . Следовательно, . Ответ:

13. Найти сумму ряда:.

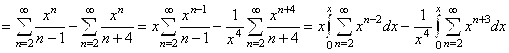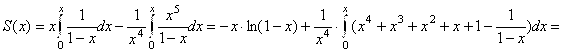
Обозначим сумму ряда через S(X). Тогда . Но есть суммы бесконечно убывающих геометрических прогрессий при . Следовательно, . Ответ: .

14. Получить решение дифференциального уравнения 1-го и 2-го порядков в виде степенного ряда или ряда Тейлора:

Будем искать решение уравнения в виде , где . Будем последовательно вычислять производные : . Следовательно, . Таким образом, . Ответ: .

15. Получить решение дифференциального уравнения 1-го и 2-го порядков в виде степенного ряда или ряда Тейлора:

Будем искать решение уравнения в виде , где . Будем последовательно вычислять производные : . Следовательно, . . Таким образом, .

Ответ: .

16. Разложить заданную графиком периодическую функцию в ряд Фурье:

По графику определяем .

Разложение функции в ряд Фурье имеет вид: . Вычислим коэффициенты : . Вычислим коэффициенты : .

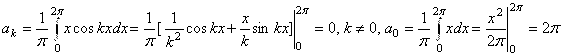Таким образом, . Ответ: .

17. Разложить функцию в ряд Фурье на :

Вычисляем коэффициенты разложения данной функции в ряд Фурье. Так как функция чётная, то все , . Из таблиц находим (при ): . Таким образом,

. Ответ: .

18. Найти разложение функции ряд Фурье в комплексной форме на : .

В комплексной форме ряд Фурье функции периода имеет вид: где 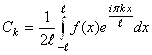. В данном случае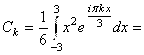 . Таким образом, .

Ответ: .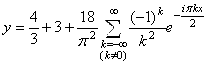

19. Функцию представить интегралом Фурье в действительной форме:

.

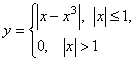Представление функции интегралом Фурье в действительной форме имеет вид 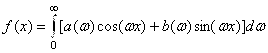, где 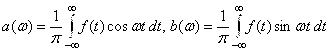. Заданная функция является чётной и, следовательно,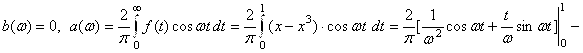 . Таким образом, .

Ответ:

20. Функцию представить интегралом Фурье в комплексной форме:

.

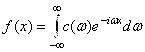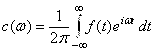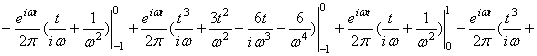
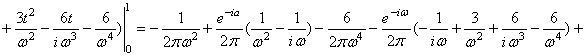
Представление функции интегралом Фурье в комплексной форме имеет вид , где . Вычислим : . Таким образом, .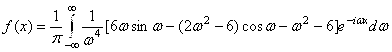

Ответ:

< Предыдущая		Следующая >