Вариант 25
1.25. Определить, при каком х функция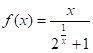 
является бесконечно малой и (или) бесконечно большой:
А) Знаменатель дроби 
при действительных значениях х. Следовательно, функция 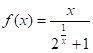не является бесконечно большой ни при каких значениях х.
Б) При 
знаменатель дроби , а числитель . Следовательно,
,
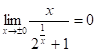Т. е. при 
функция 
является бесконечно малой.
2.25. Дать определение предела функции и изобразить схематически график функции В окрестности предельной точки.
Число 0 есть предел функции при 
,
Если для любого 
Существует такая
Окрестность точки 
, что для всех 
,
Удовлетворяющих неравенству 
,
Будет справедливо неравенство 
.
3.25. Доказать, что 
, указать 
.
По определению для любого Существует такой номер 
, что 
для всех номеров 
. Найдем такой номер
Итак, 
. Пусть 
.
Таким образом, при 
Вычислить пределы:
4.25.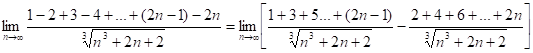 
Заметим, что в числителе обеих частей предела имеем сумму 
слагаемых арифметической прогрессии.
В первой части: 
,
Во второй части: 
Итак:
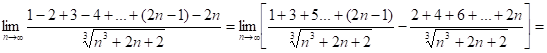
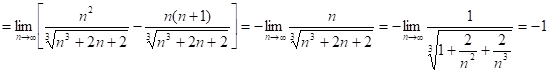
5.25. 
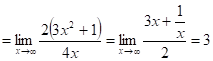
6.25.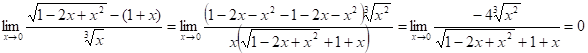 
7.25. 
8.25.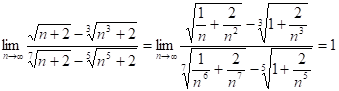 
9.25. 
10.25. 
11.25.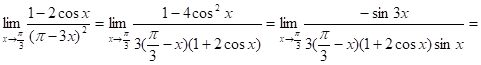 
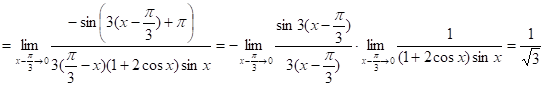
12.25.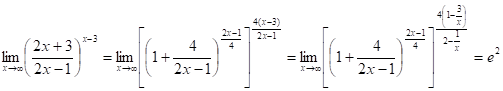 
14.25. 
Найдем отдельно
15.25. Найти точку разрыва функции, исследовать ее характер и построить график в окрестности точки разрыва:
При 
:
Следовательно, 
- точка бесконечного разрыва (2-го рода)