Вариант № 16

Вариант 16

1.16. Определить, при каком х функция является бесконечно малой и (или) бесконечно большой:

А) Знаменатель дроби при действительных значениях х. Следовательно, функция не является бесконечно большой ни при каких значениях х.

Б) При знаменатель дроби , а числитель . Следовательно,,

Т. е. при функция является бесконечно малой.

2.16. Дать определение предела функции и изобразить схематически график функции В окрестности предельной точки.

Число -1 есть предел функции при ,

Если для любого Существует такая

Окрестность точки , что для всех ,

Удовлетворяющих неравенству ,

Будет справедливо неравенство

.

3.16. Доказать, что , указать .

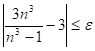По определению для любого Существует такой номер , что для всех номеров . Найдем такой номер

Итак,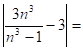

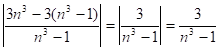
При . Пусть .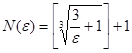

Таким образом, при

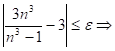
Вычислить пределы:

4.16.

Заметим, что в знаменателе имеем сумму слагаемых арифметической прогрессии с разностью :

Итак:

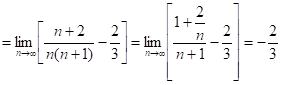
5.16.

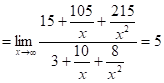
6.16.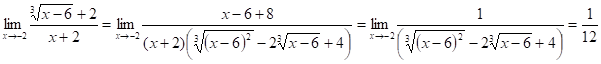

7.16.

8.16.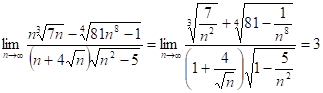

9.16.

10.16.

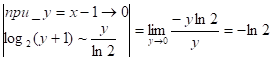
11.16.

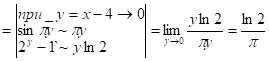
12.16.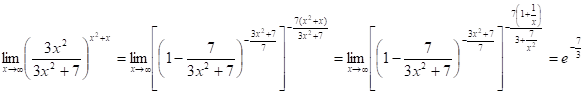

14.16.

Найдем отдельно

,

15.16. Найти точку разрыва функции, исследовать ее характер и построить график в окрестности точки разрыва:

При при

При при

Следовательно, - точки бесконечного разрыва (2-го рода)

< Предыдущая		Следующая >