Вариант № 20

1. Найти область определения функции :.

Неравенство выполняется всегда. Поэтому область определения данной функции определяется следующими неравенствами: , т. е. , и , т. е. . Решением системы этих неравенств является одна точка . Ответ: .

2. Построить график функции: .

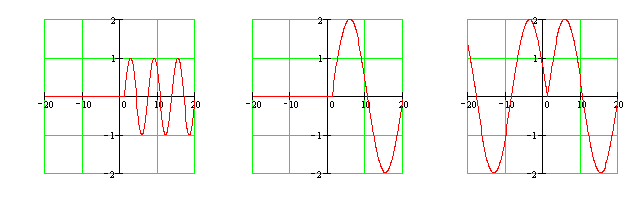
Область определения функции: . Преобразуем функцию: и . Функция чётная относительно разности . Поэтому достаточно построить правую часть графика, затем отобразить его влево зеркально относительно прямой . Строим по точкам график функции в интервале , затем «растягиваем» его по оси ОУ в два раза, а по оси OX – в три раза. Полученный график отображаем зеркально влево.

Ответ: Последовательность построения графика представлена на рисунках.

3. Построить график функции: .

Область определения функции: – вся числовая ось: . 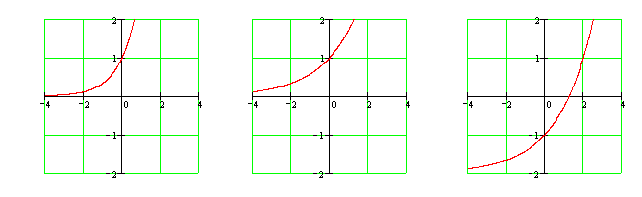Сначала построим график функции , затем «растянем» полученный график в три раза по оси OX, затем сместим его на 2 единицы вниз по оси ОY. Получим график функции . Точки пересечения с осями координат и .

Ответ: Последовательность получения графика представлена на рисунке.

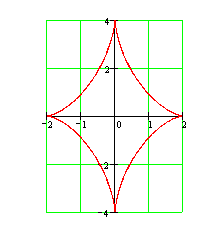4. Построить график функции: .

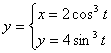Составим таблицу координат нескольких точек графика в первой четверти:

T	0	π/6	π/4	π/3	π/2
X	2	1.3	0.708	0.25	0
Y	0	0.5	1.414	2.598	4

График симметричен относительно осей координат и относительно начала координат. Поэтому нет необходимости вычислять координаты точек в других четвертях координатной плоскости. По точкам строим график и отражаем его симметрично (относительно начала координат) в другие четверти.

Ответ: График представлен на рисунке.

5. Построить график функции: .

Функция существует, когда . Так как , то достаточно построить правую половину графика, а затем отразить его зеркально в левую полуплоскость. Составим таблицу значений функции:

φ	-π/6	-π/12	0	π/6	π/4	π/3	π/2
ρ	0	0.241	0.5	1	1.207	1.366	1.5

Строим правую половину графика по этим точкам и отражаем его в левую полуплоскость.

Ответ: График представлен на рисунке.

6. Вычислить предел: .

Возведём все скобки в степени и приведём подобные:

.

Ответ: .

7. Вычислить предел: (неопределённость вида (0/0)).

Разлагаем числитель и знаменатель на простые множители:

. Ответ: .

8. Вычислить предел: (неопределённость вида (0/0)).

Умножим числитель и знаменатель на сопряжённое к знаменателю выражение: .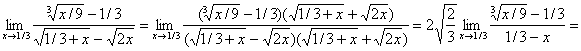

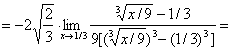
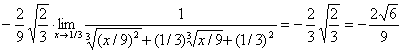Ответ: .

9. Вычислить предел: (неопределённость вида (0/0)).

Сделаем замену переменной:

. Здесь

воспользовались первым замечательным пределом: . Ответ: .

10. Вычислить предел: (неопределённость вида (1∞)).

Приведём предел ко второму замечательному пределу: :

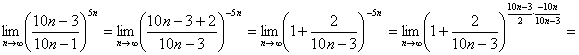
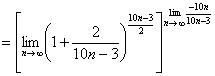. Предел в квадратных скобках равен числу E. Предел в показателе степени равен . Ответ: .

11. Вычислить предел: (неопределённость вида (0/0)).

Воспользуемся эквивалентными величинами:

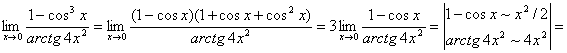
. Ответ: .

12. Исследовать функцию на непрерывность и построить эскиз графика: .

Область определения: . 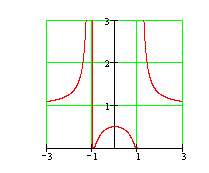В области определения функция является непрерывной (как элементарная функция). Исследуем поведение функции в граничных точках области определения: . Таким образом, в точках X= -1 и X=1 функция имеет разрывы второго рода. Для построения эскиза графика функции рассмотрим поведение функции в бесконечности: .

Ответ: В точках X= -1 и X=1 функция имеет разрывы второго рода, в остальных точках она непрерывна. Эскиз графика представлен на рисунке.

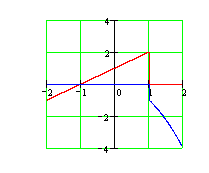
13. Исследовать функцию на непрерывность и построить эскиз графика: .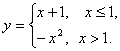

Область определения функции: . Ось ОХ разбивается на два интервала, на каждом из которых функция F(X) совпадает с одной из указанных непрерывных функций. Поэтому точкой разрыва может быть только точка, разделяющая интервалы. Вычислим односторонние пределы:

. Таким образом, в точке X=1 функция терпит разрыв первого рода. Величина скачка функции в точке X=0 равна -3.

Ответ: В точке X=1 функция имеет разрыв первого рода, в остальных точках она непрерывна. Эскиз графика представлен на рисунке.

14. Исходя из определения производной, найти :

.

По определению . Заменим ΔX на X-X0:

. Но , поэтому . В данном случае .

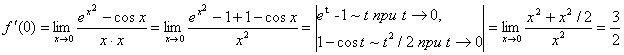Ответ: .

15. Найти производную показательно-степенной функции: . Прологарифмируем функцию: . Берём производную, как производную неявной функции: . Подставляем сюда Y: . Ответ: .

16. Составить уравнения касательной и нормали к кривой в данной точке, вычислить :

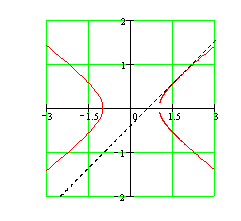
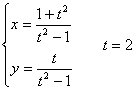. Уравнения касательной и нормали к кривой имеют вид и , где и - координаты точки касания. Вычислим сначала эти координаты:

. Найдём производные и : . Тогда . Далее, 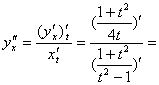, следовательно, . Таким образом, уравнение касательной , уравнение нормали . Или и . Ответ:

17. Функция Y(X), заданная неявно уравнением , принимает в точке значение . Найти .

Дифференцируем уравнение по X, предполагая, что Y= Y(X): . Из этого равенства находим: . Находим вторую производную: . Вычислим производные в точке : . Ответ: , , .

18. Вычислить приближённое значение функции в заданной точке с помощью дифференциала: .

По определению дифференциала или, в других обозначениях, . Отсюда получаем формулу для приближённых вычислений: . В данном случае . Тогда . Ответ:

19. Вычислить предел с помощью правила Лопиталя: .

Это неопределённость вида (00). Преобразуем предел:

. Найдём предел в показателе степени:

. Следовательно,

. Ответ: .

20. Вычислить предел с помощью правила Лопиталя: .

Это неопределённость вида (∞∙0):

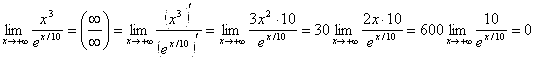
. Ответ: .

21. Многочлен по степеням X представить в виде многочлена по степеням : .

Запишем формулу Тейлора для многочлена четвёртой степени: .

Найдём все производные: , . Тогда . Подставив это в формулу, получим: .

Ответ: .

22. Найти многочлен, приближающий заданную функцию в окрестности точки X0 с точностью до : .

Применяем формулу Тейлора:

.

Вычисляем последовательно:

.

Ответ:

23. Исследовать поведение функции в окрестности точки с помощью формулы Тейлора: .

Найдём значения функции и её первых четырёх производных в заданной точке:

,. По формуле Тейлора .

Ответ: В окрестности точки (1, 1) функция ведёт себя как степенная функция четвёртой степени. Точка (1, 1) является точкой максимума.

24. Вычислить предел с помощью формулы Тейлора: .

Преобразуем числитель: . Следовательно, . Сделаем замену: . Тогда . По формуле Тейлора . Подставим это

В предел: .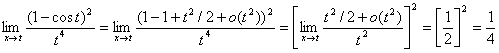

Ответ: .

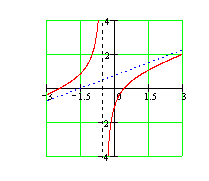
25. Найти асимптоты и построить эскиз графика функции: .

Область определения функции: . Функция непрерывна в каждой точке области определения. Найдём односторонние пределы в граничной точке области определения: . Отсюда следует, что прямая является вертикальной асимптотой. Исследуем функцию при :. Ищем наклонные асимптоты в виде : . Следовательно, прямая является наклонной асимптотой. Ответ: Эскиз графика представлен на рисунке.

26. Провести полное исследование поведения функции и построить её график: .

1. Область определения: .

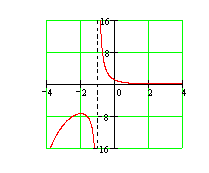2. Чётность, нечётность, периодичность отсутствуют. 3. Функция имеет разрыв в точке . Исследуем поведение функции в окрестности точки разрыва: . Таким образом, прямая является вертикальной асимптотой.

4. (по правилу Лопиталя). Ищем наклонные асимптоты в виде : . Следовательно, прямая является правосторонней горизонтальной асимптотой. Других асимптот нет.

5. Первая производная . Производная обращается в нуль в точке . Слева от точки производная положительна, справа отрицательна. Следовательно, в точке имеет место максимум функции, причём . В точке производная имеет разрыв. В интервале функция монотонно возрастает, в интервале функция монотонно убывает, в интервале функция монотонно убывает.

6. Вторая производная: 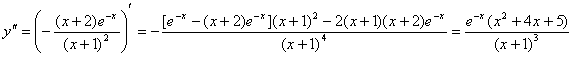. Знак второй производной определяется знаменателем (числитель всегда положительный). Если , то производная отрицательна и, следовательно, интервал - интервал выпуклости графика функции. В интервале производная положительна, следовательно, это интервал вогнутости графика функции. Точек перегиба нет. 7. График функции не пересекает осей координат.

Ответ: График функции представлен на рисунке, экстремум – максимум – в точке . Вертикальная асимптота , правосторонняя горизонтальная асимптота .

< Предыдущая		Следующая >