Вариант № 16
Задача 1
Используя определение производной, найти ![]() для функции
для функции ![]() в точке
в точке ![]()
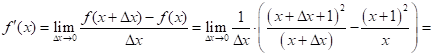
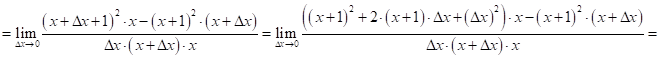
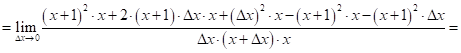
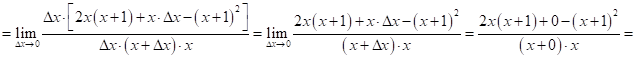
![]()
Задача 2
2.1 ![]()
![]()
2.2 ![]()
![]()
2.3 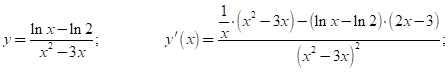
2.4 ![]()
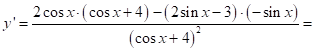
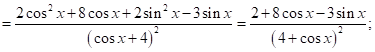
2.5 

2.6 
2.7 ![]()

2.8 ![]()
2.9 ![]()
![]()
2.10 ![]()

2.11 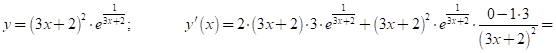
![]()
2.12 ![]()
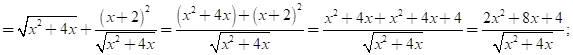
2.13 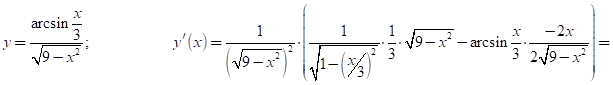
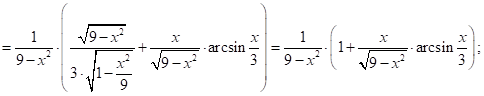
2.14 ![]()
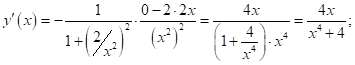
2.15 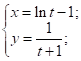
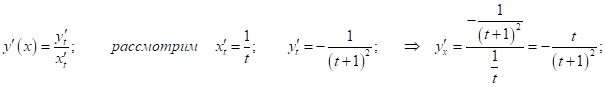
2.16
![]() Продифференцируем по X равенство (1):
Продифференцируем по X равенство (1):
![]()
2.17
![]() прологарифмируем равенство (1):
прологарифмируем равенство (1):
![]()
![]()
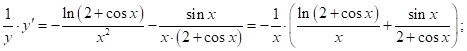

Задача 3
Написать уравнения касательной ![]() И нормали
И нормали ![]() к кривой
к кривой![]() :
: ![]()
В точке ![]()
А) уравнение касательной к кривой L в точке ![]() :
: ![]() ;
;
Найдем ![]()
![]()
![]() Уравнение искомой касательной (K):
Уравнение искомой касательной (K): ![]() или
или ![]()
Б) уравнение нормали ![]() к кривой L в точке
к кривой L в точке ![]() :
: ![]() ;
;
Т. е. ![]() или
или ![]()
Задача 4 (смотри рис. 4)
Составить уравнение касательной к кривой ![]() , зная, что эта касательная перпендикулярна прямой
, зная, что эта касательная перпендикулярна прямой ![]() Сделать чертёж.
Сделать чертёж.
Пусть искомая касательная (K) проходит через точку ![]() , тогда её уравнение:
, тогда её уравнение: ![]()
Вычислим ![]() , для чего продифференцируем по х равенство (1):
, для чего продифференцируем по х равенство (1):
![]()
![]()
![]()
По условию, искомая касательная (K) перпендикулярна прямой (M) , следовательно
![]()
Точка ![]() Следовательно можно записать:
Следовательно можно записать: ![]()
Решим совместно уравнения (2), (3) и найдём координаты точки ![]() :
:
![]()
![]()
![]()
![]()
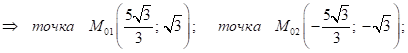
Следовательно, уравнения искомых касательных ![]()
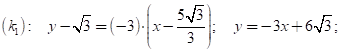

![]()
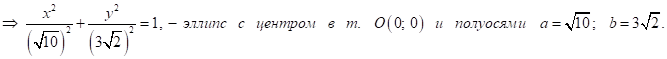
Задача 5
Найти производные второго порядка для функций, заданных в пунктах 2.14, 2.15, 2.16.
2.14 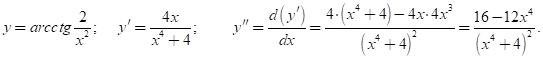
2.15 
![]()
![]()


2.16 ![]() продифференцируем равенство (1) по X:
продифференцируем равенство (1) по X:
![]()
Продифференцируем равенство (2) по X: ![]()
![]()
![]() , Где
, Где ![]()
Задача 6
Закон движения материальной точки : ![]()
![]()
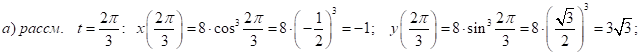
![]()
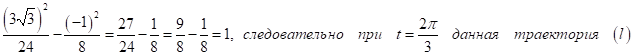
![]()
![]()
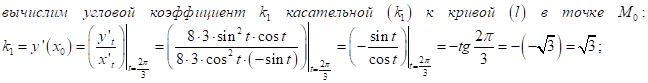
![]()
![]()
![]()
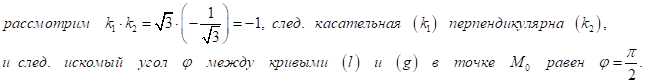
![]()
Задача 7 Закон прямолинейного движения материальной точки:
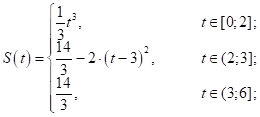 1)
1) 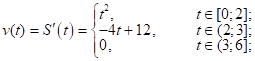
2) ![]() 3)
3) 
4) Точка находится в покое при ![]()
5) Точка имела набольшую скорость ![]() в момент времени T = 2 C .
в момент времени T = 2 C .
Задача 8
Закон движения материальной точки:
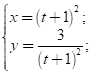
![]()
Определим момент времени ![]() , соответствующий точке
, соответствующий точке![]()
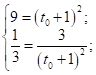
![]()
Скорость движения проекции точки на ось OY :
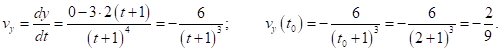
Задача 9
Зависимость количества растворяющегося вещества от времени : ![]()
Где ![]()
![]()
![]()
![]()
Рассм. ![]()
![]()
Задача 10
Найти дифференциалы: ![]()
Применим формулу ![]()
A) ![]()
![]()
Б) ![]()
![]()
В) ![]()
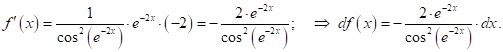
Задача 11
Вычислить приближенно с помощью дифференциала значение функции ![]()
В точке ![]()
Рассмотрим точку ![]()
Рассмотрим ![]()

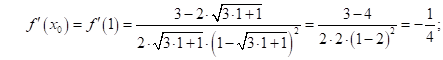
![]()
![]()
| < Предыдущая | Следующая > |
|---|