Вариант № 03
Задача 1
Используя определение производной, найти ![]() для функции
для функции ![]() .
.
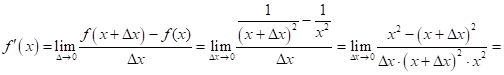
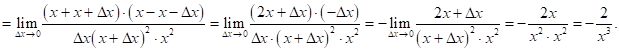
Задача 2
Найти производные следующих функций:
2.1 ![]()
![]()
2.2 y=![]() ;
; ![]() ;
;
2.3 y=![]()

2.4 Y=![]()
![]()
2.5 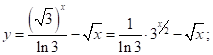
![]()
2.6 ![]()
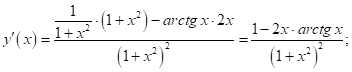
2.7 Y=![]()

2.8 Y=![]()
![]()
2.9 Y=![]()

2.10 y=![]()
![]()
2.11 ![]()
![]()
![]()
2.12 y=![]()
![]()
2.13 y=![]()
![]()
2.14 y=![]()

2.15 ![]()
![]() вычислим
вычислим 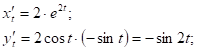
![]()
2.16 2Y+1=![]() (1) продифференцируем равенство (1) по х:
(1) продифференцируем равенство (1) по х:
![]()
![]()
![]()
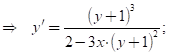
2.17 Y=![]() рассмотрим Ln Y = 3X
рассмотрим Ln Y = 3X![]() (1)
(1)
Продифференцируем по х равенство (1):
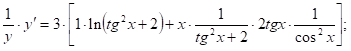
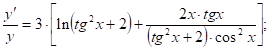

Задача 3 (смотри рис. 3)
Написать уравнения касательной![]() и нормали
и нормали![]() к кривой
к кривой![]() :
: ![]() (1) в точке М
(1) в точке М![]() Сделать чертеж.
Сделать чертеж.
А) уравнение касательной ![]() К кривой
К кривой![]() : Y = Y(X) в точке М
: Y = Y(X) в точке М![]() имеет вид:
имеет вид:
![]() найдем
найдем ![]() , для чего продифференцируем по х равенство (1):
, для чего продифференцируем по х равенство (1):
![]()
![]()
![]()
![]()
![]() Уравнение касательной
Уравнение касательной![]() :
: ![]()
![]() Или
Или ![]()
Б) уравнение нормали ![]() К кривой
К кривой![]() : Y = Y(X) в точке М
: Y = Y(X) в точке М![]() имеет вид:
имеет вид:![]()
![]()
![]() или
или ![]() .
.
Задача 4
Составить уравнение касательной ![]() К кривой
К кривой ![]() :
: ![]() (1), зная, что эта касательная перпендикулярна прямой
(1), зная, что эта касательная перпендикулярна прямой![]() :
: ![]() или
или ![]() ;
;
Пусть искомая касательная (K) проходит через точку М![]() Тогда ее уравнение имеет
Тогда ее уравнение имеет
Вид: Y-![]() найдем
найдем ![]()
![]()
![]()
По условию задачи (K)![]() (M), след.,
(M), след., ![]() т. е.
т. е. ![]()
![]()
Нах-м ![]() из равенства (1):
из равенства (1): ![]() опр - м
опр - м 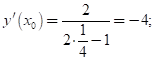
![]() Уравнение касательной
Уравнение касательной ![]() :
: ![]()
![]()
Задача 5
Найти производные второго порядка для функций, заданных в пунктах 2.14, 2.15, 2.16.
2.14 ![]()
![]()

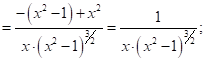
2.15 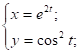
![]()
![]()
![]() применим ф – лу:
применим ф – лу: 
Вычислим: 
![]()
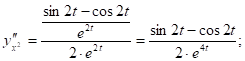
2.16 2Y+1=X![]() (1)
(1)
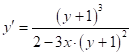 ; (2) (смотри рещ – е зад. 2.16);
; (2) (смотри рещ – е зад. 2.16);
Продифференцируем по х равенство (1):
![]()
Продифференцируем по х равенство (3):
![]()
![]()
![]()
 , где
, где 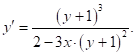
Задача 6
Закон движения материальной точки: ![]()
Показать, что при T = ![]() траектория (L) движения точки пересекает параболу
траектория (L) движения точки пересекает параболу![]()
И найти угол между траекторией и параболой.
А) рассм. ![]()
![]() Y
Y![]()
![]() , т. е. при T=
, т. е. при T=![]() (т. е. в т.
(т. е. в т.![]() траектория движения (L) пересекает параболу Y=
траектория движения (L) пересекает параболу Y=![]()
Б) рассмотрим касательную к траектории (L) в т.![]() : ее угловой коэффициент K
: ее угловой коэффициент K![]() ,
,
Где ![]()
![]()
![]()
![]()
Рассмотрим параболу ![]()
![]() следовательно угловой коэффициент касательной к параболе в т.
следовательно угловой коэффициент касательной к параболе в т.![]() равен
равен ![]()
В) угол между этими двумя касательными находим по формуле:
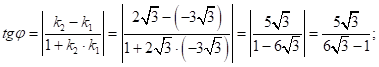
![]()
![]()
![]()
Задача 7 (смотри рис. 7)
Закон прямолинейного движения материальной точки:
 1) V(T)=
1) V(T)=
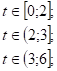
2) V(T![]()
![]()
3) 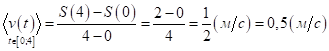 ;
;
4) точка находилась в покое при ![]() ;
;
5) точка имела наибольшую скорость ![]() в момент времени T = 2 C.
в момент времени T = 2 C.
Задача 8 (смотри рис. 8)
Закон движения материальной точки:
Но ![]() или
или ![]() , - траектория(L) движения материальной точки (парабола);
, - траектория(L) движения материальной точки (парабола);
Находим значение ![]() , соответствующее т.
, соответствующее т.![]()

![]()
Скорость изменения ординаты:
![]()
![]() .
.
Задача 9
Зависимость угла поворота от времени: ![]()
Коэффициент а найдем из условия: ![]() т. e.
т. e. ![]()
![]() Зависимость
Зависимость![]() имеет вид:
имеет вид:![]()
Рассмотрим угловую скорость шкива: ![]()
![]()
Задача 10
Найти дифференциалы: ![]()
![]()
![]()
Применим формулу:![]()
A) F(x)=![]()
![]()
Б) F(X)=Sin5X; ![]()
В) ![]()
![]()
Задача 11
Вычислить приближенно с помощью дифференциала значение функции ![]()
В точке х=4,02;
Рассмотрим точку ![]()
![]()
Вычислим 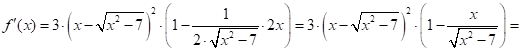
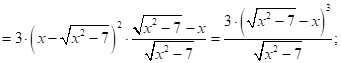
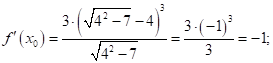
![]()
![]()
| < Предыдущая | Следующая > |
|---|