Вариант контрольной 12

Вариант 12

Задача 1. Вычислить определенный интеграл методом замены переменной с точностью до двух знаков после запятой.

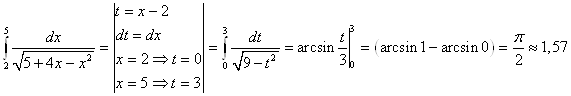
Задача 2. Вычислить определенный интеграл методом интегрирования по частям с точностью до двух знаков после запятой.

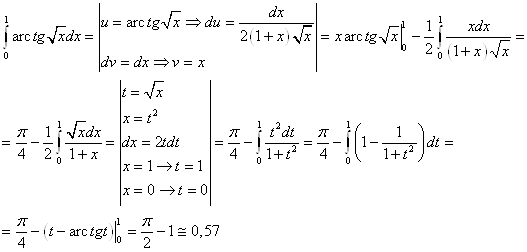
Задача 3. Вычислить определенный интеграл с точностью до двух знаков после запятой, выделяя в знаменателе полный квадрат.

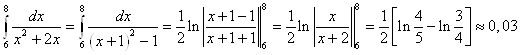
Задача 4. Вычислить площадь фигуры, ограниченной графиками функций:

Решение.

Находим точки пересечения графиков функций:

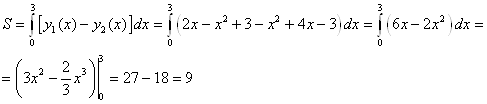
Задача 5. Вычислить площадь фигуры:

Решение.

Задача 6. Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями в полярных координатах.

Решение:

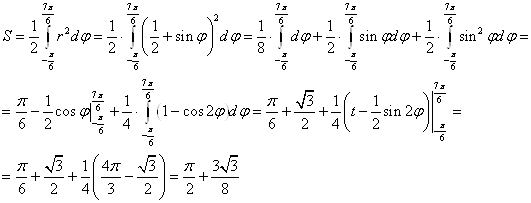
Задача 7. Вычислить длину дуги кривой:

Решение.

Задача 8. Вычислить длину дуги кривой:

;

Решение.

Задача 9. Вычислить длину дуги кривой:

;

Решение.

Задача 10. Вычислить объём тела, ограниченного поверхностями ,

Решение: Имеем тело (эллиптический параболоид) с сечениями параллельно XOY, зависящими только от Z:.

Значит, объем тела:

Сечение, перпендикулярное оси OZ – эллипс:

Площадь эллипса:

Задача 11. Вычислить объем тела, образованного вращением фигуры, ограниченной графиками функций. Ось вращения OХ.

Решение: Ось вращения OХ не пересекает заданную фигуру (круг).

Значит, согласно второй теореме Гульдена,

Объем тела вращения вокруг оси Ох равен

Произведению площади данного круга

На длину окружности, описываемой

Центром тяжести фигуры.

Центр тяжести круга находится в центре круга.

Значит, длина окружности равна .

Площадь данного круга равна:

Значит, объем тела, образованного вращением данного круга равен:

Задача 12. Найти координаты центра масс однородной плоской кривой L: кривая от точки До точки .

Решение: В точке , в точке

Задача 13. Найти статический момент относительно оси Ох дуги синусоиды .

Решение: Статический момент относительно оси Ох:

Задача 14. Вычислить несобственные интегралы или доказать их расходимость:

А)

Подынтегральная функция определена и непрерывна при . Значит, несобственный интеграл:

Несобственный интеграл сходится.

Б)

Подынтегральная функция определена и непрерывна при и При . Значит, несобственный интеграл:

Несобственный интеграл сходится.

Задача 15. Исследовать сходимость интеграла от неотрицательной функции

Подынтегральная функция определена и непрерывна при и Не Определена при . Значит, несобственный интеграл имеет особенности на обеих границах интегрирования. Представим заданный интеграл в виде:

Оценим подынтегральную функцию первого интеграла при :

Поскольку интеграл 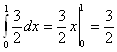сходится, то по признаку сравнения сходится первый несобственный интеграл.

Оценим подынтегральную функцию второго интеграла:

справедлива для всех .

Поскольку интеграл 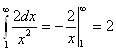сходится, то по признаку сравнения сходится второй несобственный интеграл.

Следовательно, сходится исходный несобственный интеграл

< Предыдущая		Следующая >