Вариант № 11
Задача 1.
![]() , (1) – ур-е с раздел. перем.;
, (1) – ур-е с раздел. перем.;

![]() – общий интеграл ур-я (1).
– общий интеграл ур-я (1).
Задача 2.
![]()
Ур-е (1) – ур-е с раздел. перем.: ![]()
![]()
![]()
![]() общий интеграл ур-я (1) имеет вид:
общий интеграл ур-я (1) имеет вид: ![]()
Пост. C опр-м из нач. усл. (2): ![]()
![]() инт-л зад. Коши (1), (2) :
инт-л зад. Коши (1), (2) : ![]() .
.
Задача 3.

Ур. (2)- однор. ур-е. Введём новую неизвестную ф-ю ![]() тогда
тогда ![]()
![]()
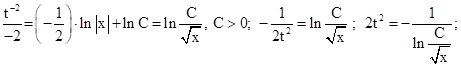


Задача 4.

Введём новую неизв. ф-ю ![]() , тогда
, тогда ![]()
![]()

![]()

![]()
Задача 5.
![]() лин. неоднор. ур-ие 1 пор.;
лин. неоднор. ур-ие 1 пор.;
Рассм. соотв. однор. ур.: ![]()

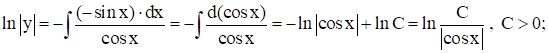

![]() - общ. реш. одн. ур-я (2);
- общ. реш. одн. ур-я (2);
Общ. реш-е неодн. ур-я (1) ищем в виде (метод вариации произв. пост-х):  ;
;
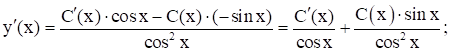
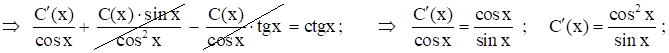
 ;
;
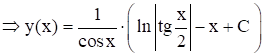 - общее реш-е ур-я (1)
- общее реш-е ур-я (1)
Задача 6.

Ур. (2) - лин. неодн. ур-ие 1 пор.; рассм. соотв. однор ур.: ![]()
![]()
![]()
![]() , - общ. реш. одн. ур-я (3);
, - общ. реш. одн. ур-я (3);
Общ. реш. неодн. ур. (2) ищем в виде (метод вариации произв. пост.):![]()
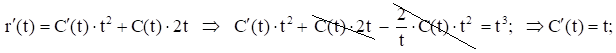
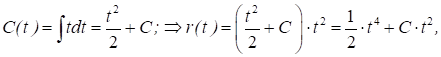 - общ. реш. неодн. ур. (2) и след. ур. (1).
- общ. реш. неодн. ур. (2) и след. ур. (1).
Задача 7.

Ур. (1) – ур. Бернулли ![]() ; применим метод Бернулли, т. е. положим
; применим метод Бернулли, т. е. положим ![]() ,
,
тогда ![]()
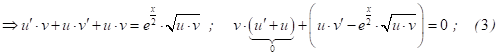
Рассм. вспомогат. диф. ур.: ![]() - ур-е с разд. перем;
- ур-е с разд. перем;

Рассм. частн. реш. ![]() ур-я (4) и подст. его в ур-е (3):
ур-я (4) и подст. его в ур-е (3):
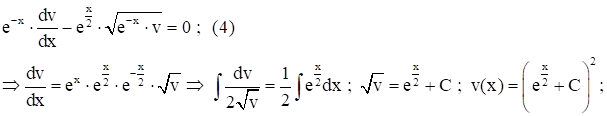
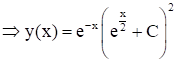 - общ. реш. ур. (1); пост. C опр-м из нач. усл. (2):
- общ. реш. ур. (1); пост. C опр-м из нач. усл. (2):
![]()
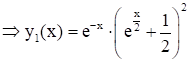 - реш-е зад. Коши (1), (2).
- реш-е зад. Коши (1), (2).
Задача 8.
![]()
Ур. (1) не содержит явно неизв. ф-ю Y(X); введём новую неизв. ф-ю ![]() тогда
тогда ![]()
![]()


![]()
![]() - общ. реш. ур. (2);
- общ. реш. ур. (2);
Рассм. теперь
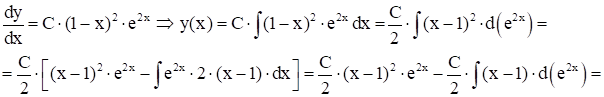
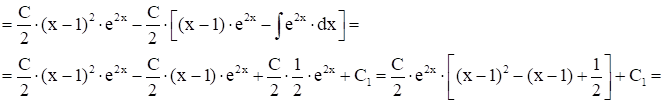
 - общее реш-е ур-я (1).
- общее реш-е ур-я (1).
Задача 9.
![]()
Ур. (1) не содержит явно неизв. ф-цию Y(X); введём новую неизв. ф-ю ![]() тогда
тогда ![]()
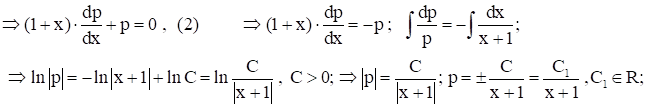
![]() - общ. реш. ур. (2); рассм. теперь
- общ. реш. ур. (2); рассм. теперь ![]()
![]() , - общ. реш. ур-я (1).
, - общ. реш. ур-я (1).
Задача 10.

Ур. (1) не содержит явно аргумент X; введём новый аргум. Y и новую неизв-ю ф-ю ![]()
Тогда


Пост-ю С опр-м из усл-я:
При X=0 Y=0 и ![]() т. е. можно записать:
т. е. можно записать:![]()
![]()
(возможен лишь знак “+”) ![]()
![]() - общ. реш. ур-я (4);
- общ. реш. ур-я (4);
Рассм. теперь: 
Пост. ![]() определим из нач. усл. (2): при X=0, Y=0, т. е.:
определим из нач. усл. (2): при X=0, Y=0, т. е.: ![]()
![]() - реш-е зад Коши (1) – (3).
- реш-е зад Коши (1) – (3).
Задача 11.
![]() - лин. однор. ур. 2-го пор. с пост. коэф.;
- лин. однор. ур. 2-го пор. с пост. коэф.;
Рассм. хар. ур.: ![]()
![]()
След. фунд. с-му реш-й ур-я (1)образуют ф-ии ![]() и
и ![]() ;
;
Общ. реш. ур-я (1) имеет вид: ![]()
Задача 12.
![]() т.
т. ![]() прямая (M): Y = 4.
прямая (M): Y = 4.
Найти интегр. кривую (L) ур-я (1), к-рая касается прямой (M) в т. ![]() .
.
Так как искомая кривая (L) (y=Y(X)) ур-я (1) проходит через т. ![]()
То можно записать: y(0)=4 , (2); т. к. эта кривая (L) в т. ![]() касается прямой (M) (Y = 4), то вып-ся усл-е:
касается прямой (M) (Y = 4), то вып-ся усл-е: ![]() След., данная задача предст. собой задачу Коши (1) – (3) для ур-я (1).
След., данная задача предст. собой задачу Коши (1) – (3) для ур-я (1).
Ур. (1) – мин. однор. ур. 2-го пор. с пост. коэф.; рассм. хар. ур.: ![]()
 след. общ. реш-е ур-я (1) имеет вид:
след. общ. реш-е ур-я (1) имеет вид:
![]()
Рассм 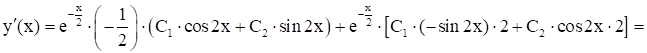
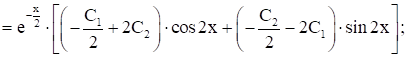
Нах-м теперь пост. ![]() из нач. усл-й (2), (3):
из нач. усл-й (2), (3):

![]()
![]() Ур-е искомой интегр. Rривой ур-я (1) имеет вид:
Ур-е искомой интегр. Rривой ур-я (1) имеет вид: ![]()
Задача 13
![]() - лин. однор. диф. ур. 2 пор. с пост. коэф. ;
- лин. однор. диф. ур. 2 пор. с пост. коэф. ;
хар. ур. для ур – я (1): ![]()
След., фунд. с – му реш – й ур – я (1) образуют ф – и ![]() ;
;
![]() общ. реш. ур. (1) имеет вид:
общ. реш. ур. (1) имеет вид: ![]() .
.
Задача 14
![]() - лин. однор. диф. ур. 4 пор. с пост. коэф. ;
- лин. однор. диф. ур. 4 пор. с пост. коэф. ;
Хар. ур. для ур – я (1): ![]() ,
,
След., фунд. с – му реш – й ур – я (1) образуют ф – и ![]() ;
;
Опр – ль Вронского для фунд. с – мы реш – й: ![]()

![]() , след., с – ма ф – й
, след., с – ма ф – й ![]() линейно независима;
линейно независима;
Общ. реш. ур. (1) имеет вид: ![]() .
.
Задача 15
![]()
- лин. неоднор. диф. ур. 3 пор. с пост. коэф. и со спец. правой частью (квазимногочлен);
Соотв. однор. диф. ур.: ![]()
хар. ур. для ур – я (2): ![]() ;
;
Общ. реш. однор. ур. (2) имеет вид: ![]() ;
;
Структура общего реш – я неоднор. ур - я (1) имеет вид: ![]() ;
;
Где ![]() - общ. реш. однор. ур. (2), а функции
- общ. реш. однор. ур. (2), а функции ![]() суть, соответственно, частные реш – я
суть, соответственно, частные реш – я
След. ур – й: ![]()
![]() ;
;
![]() , причём частные реш – я
, причём частные реш – я ![]() Ищем в виде:
Ищем в виде:
![]() .
.
Задача 16
 - зад. Коши.
- зад. Коши.
Ур – е (1)- лин. неоднор. диф. ур. 3 пор. с пост. коэф. и со спец. правой частью (многочлен);
Соотв. однор. диф. ур.: ![]()
хар. ур. для ур – я (5): ![]() ;
;
Общ. реш. однор. ур. (5) имеет вид: ![]() ;
;
Частное реш – е ![]() неоднор. диф. ур. (1) ищем в виде:
неоднор. диф. ур. (1) ищем в виде: ![]() ;
;
Рассм. ![]()
![]()
![]()
![]()
Общее реш – е неоднор. ур - я (1) имеет вид: ![]() ;
;
Рассм. ![]() ;
; ![]() ;
;
Опр – м пост. ![]() из нач. усл – й (2), (3), (4):
из нач. усл – й (2), (3), (4):
![]() ;
;
![]() ;
;
![]() ;
;
Решим с-му ур-й (6), (7), (8) и опр-м пост. ![]() :
: ![]() ;
;
![]() Реш. зад. Коши (1) - (4):
Реш. зад. Коши (1) - (4): ![]() .
.
Задача 17
![]()
- лин. неоднор. диф. ур. 2 пор. с пост. коэф. и со спец. правой частью (квазимногочлен);
Соотв. однор. диф. ур.: ![]()
Хар. ур. для ур – я (2): ![]() ;
;
Общ. реш. однор. ур. (2) имеет вид: ![]() ;
;
Структура общего реш – я неоднор. ур - я (1) имеет вид:
![]() ; где
; где ![]() - общ. реш. однор. ур. (2), а
- общ. реш. однор. ур. (2), а ![]() - частное реш – е неодн. ур – я (1),
- частное реш – е неодн. ур – я (1),
Которое ищем в виде: ![]() ; рассм.
; рассм. ![]()
![]() ;
;
![]() ;
; ![]() ;
;
Общее реш – е неоднор. ур - я (1) имеет вид: ![]() .
.
Задача 18
![]()
- лин. неоднор. диф. ур. 2 пор. с пост. коэф. и со спец. правой частью (квазимногочлен);
Соотв. однор. диф. ур.: ![]() хар. ур. для ур – я (2):
хар. ур. для ур – я (2): ![]() ;
;
Общ. реш. однор. ур. (2) имеет вид: ![]() ;
;
Структура общего реш – я неоднор. ур - я (1) имеет вид: ![]() ;
;
Где ![]() - общ. реш. однор. ур. (2), а
- общ. реш. однор. ур. (2), а ![]() - частное реш – е неодн. ур – я (1), которое ищем в виде:
- частное реш – е неодн. ур – я (1), которое ищем в виде:
![]() ; рассм.
; рассм. ![]()
![]() ;
;
![]() ;
;
![]()
Общее реш – е неоднор. ур - я (1) имеет вид: ![]() .
.
Задача 19
![]() - лин. неоднор. диф. ур. 2 пор. с пост. коэф.;
- лин. неоднор. диф. ур. 2 пор. с пост. коэф.;
Соотв. однор. диф. ур.: ![]()
хар. ур. для ур – я (2): ![]() ;
;
След., фунд. с – му реш – й ур – я (2) образуют ф – и ![]() ;
;
А общ. реш. однор. ур. (2) имеет вид: ![]() ;
;
Общ. реш. неоднор. ур. (1) будем искать методом вариации произвольных постоянных,
То есть в виде ![]() ,
,
А неизвестные ф – и ![]() опр – м из с – мы ур – й:
опр – м из с – мы ур – й:
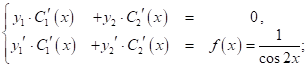

Рассм. ![]()
![]() ;
;
![]()
![]() ;
;
Общее реш – е. ур - я (1) имеет вид: ![]() .
.
| < Предыдущая | Следующая > |
|---|