Глава 09. Системы N линейных уравнений с N неизвестными. Формулы Крамера

Рассмотрим систему уравнений, у которой число уравнений совпадает с числом неизвестных (N = M):

(1.9.1)

Предположим, что определитель основной матрицы системы (или главный определитель системы) отличен от нуля:

(1.9.2)

Можно доказать, что такая система уравнений имеет единственное решение, определяемое по формулам, называемым Формулами Крамера:

(1.9.3)

Где

…,

(1.9.4)

Матрицы Bi (I = 1, 2, …, N) получаются из матрицы A заменой I–го столбца столбцом свободных членов.

Пример

Решить систему уравнений с помощью формул Крамера:

Решение

Вычислим главный определитель системы:

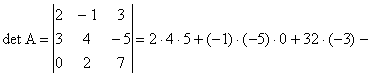
Теперь вычислим определители матриц B1, B2, B3:

Применяя формулы Крамера для определения решений, получаем:

Проверкой можно убедиться в верности найденного решения.

< Предыдущая		Следующая >
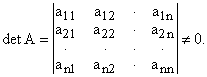
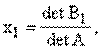