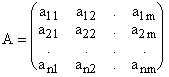Глава 08. Системы линейных алгебраических уравнений.. Основные понятия и определения

Определение

Система уравнений вида

(1.8.1)

Называется Системой n линейных уравнений с m неизвестными X1, X2, … Xm. Здесь Aij и Bj (I = 1, 2, …, N; J = 1, 2, …, M) – произвольные числа, называемые соответственно Коэффициентами при переменных И Свободными членами уравнений (1.8.1).

(1.8.2)

Называется Основной матрицей системы.

Система уравнений, все свободные члены Bi (I = 1, 2, …, N) которой равны нулю, называется Однородной.

Решением системы называется такая совокупность значений неизвестных X1 = a1, X2 = a2, …, XM = am, при подстановке которых в систему (1.8.1) каждое из ее уравнений обращается в верное равенство.

Определение

Система уравнений, имеющая хотя бы одно решение, называется Совместной. Система, не имеющая ни одного решения, называется Несовместной. Совместная система уравнений имеет либо Одно решение, и в таком случае она называется Определенной, либо, если у нее Больше одного решения, она называется Неопределенной.

Пример

Система уравнений – Совместная и определенная, так как имеет единственное решение. Система уравнений – Несовместная, а система уравнений – Совместная и неопределенная, так как имеет бесконечное множество решений.

Однородная система имеет по крайней мере Одно Решение – нулевое:

X1 = 0, X2 = 0, …, Xm = 0.

(1.8.3)

Решить систему уравнений – значит найти ее решение или доказать, что система решений не имеет.

< Предыдущая		Следующая >