Глава 07. Ранг матрицы

Рассмотрим прямоугольную матрицу (1.1.1), содержащую N строк и M столбцов. Выделим в ней произвольным образом квадратную матрицу K–го порядка. Определитель этой матрицы называется Минором K–го порядка матрицы А. Очевидно, что в общем случае таких миноров K–го порядка может быть несколько, а максимальный порядок миноров равен минимальному из чисел M и N, т. е. K £ min(N; M). Далее, из всех возможных миноров матрицы А Выделим те из них, которые Отличны от нуля. В свою очередь, среди этих миноров можно найти по крайней мере один минор наибольшего порядка.

Определение

Наибольший порядок отличных от нуля миноров называется Рангом матрицы А. Ранг матрицы обозначается rangA или r(A).

Из определения следует:

1.Ранг матрицы A Не превосходит меньшего из ее размеров, т. е. K £ min(N; M).

2.Ранг матрицы равен нулю тогда, когда все элементы матрицы равны нулю, т. е. A=0.

3.Для квадратной матрицы N–го порядка R(A) = N тогда и только тогда, когда матрица A – невырожденная.

Пример

Вычислить ранг матрицы

.

Решение

Матрица A имеет размер 4´3, поэтому rangA £ 3. Однако, все определители матрицы A равны нулю. Следовательно, rangA £ 2. Нетрудно видеть, что максимальный порядок миноров этой матрицы, отличных от нуля, равен 2.

Определение

Отличный от нуля минор матрицы, порядок которого равен рангу матрицы, называется Базисным минором этой матрицы. Столбцы и строки этой матрицы, участвующие в образовании базисного минора, также называются Базисными.

Пример

Вычислить ранг матрицы

.

Решение

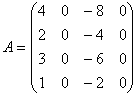Матрица A имеет четвертый порядок, поэтому R(A) £ 4. Однако |A| = 0, так как матрица A содержит нулевой столбец, поэтому R(A) £ 3. Все подматрицы третьего порядка тоже содержат нулевой столбец и поэтому имеют нулевые определители значит R(A) £ 2. Все подматрицы второго порядка либо имеют нулевой столбец (второй или четвертый), либо имеют пропорциональные столбцы (первый и третий), поэтому тоже имеют нулевые определители; таким образом R(A) £ 1. Поскольку матрица A содержит ненулевые элементы, т. е. невырожденные подматрицы первого порядка, то R(A) = 1.

В общем случае определение ранга матрицы перебором всех миноров достаточно трудоемко. Для облегчения этой задачи используются перечисленные ниже Элементарные преобразования, сохраняющие ранг матрицы.

1. Отбрасывание нулевой строки (столбца).

2. Умножение всех элементов строки (столбца) на число, не равное нулю.

3. Изменение порядка строк (столбцов), а также прибавление к каждому элементу одной строки (столбца) линейной комбинации соответствующих элементов другой строки (столбца).

4. Транспонирование матрицы.

Теорема

Ранг матрицы не изменится при элементарных преобразованиях.

< Предыдущая		Следующая >