Глава 06. Обратная матрица

Пусть дана квадратная матрица А:

.

(1.6.1)

Определение

Матрица B называется Обратной к матрице A, если A×B = B×A = E, где E – единичная матрица.

Матрица, обратная к A, обозначается A–1.

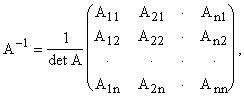
Можно доказать, что, если detA ¹ 0, то матрица A имеет обратную матрицу A–1, определяемую по формуле:

(1.6.2)

Где Aik – алгебраические дополнения к элементу Aik матрицы A (I, K = 1, 2, …, N). Построение обратной матрицы можно описать так:

1. Составим матрицу A’, написав на месте каждого элемента матрицы A его алгебраическое дополнение.

2. Разделим каждый элемент A’ на detA.

3. Транспонируем полученную матрицу.

Пример

Найти матрицу, обратную к матрице:

Решение

Следовательно матрица A–1, обратная данной существует.

.

Разделим элементы матрицы A’ на detA и транспонируем, получаем:

A11 = 4, A12 = –(–2) = 2, A21 = –1, A22 = 3. Окончательно,

Проверка:

Матрица A–1 найдена верно.

< Предыдущая		Следующая >