Глава 05. Определители высших порядков
Введем понятие определителя N–го порядка.
Определение
Определителем матрицы A N–го порядка называется Алгебраическая сумма N! произведений N–го порядка элементов этой матрицы, причем в каждое произведение входит по одному элементу из каждой строки и каждого столбца данной матрицы.
Заметим, что с ростом N резко увеличивается число членов определителя (N!). Например, для N = 4 определитель содержит 24 слагаемых. Поэтому на практике при вычислении определителей высоких порядков используют другие формулы.
Свойства определителей, рассмотренные в разделе 4, справедливы и для определителей любого порядка. Поэтому для вычисления определителей 4–го, 5–го и более высоких порядков можно воспользоваться свойством 9, сформулированное в общем случае определителя произвольного порядка носит название Теоремы Лапласа. Как нетрудно убедиться, вычисление определителя 4–го порядка сводится к вычислению четырех определителей 3–го порядка. Для облегчения решения этой задачи определитель преобразуют, используя свойство 8, стремясь получить в одном из рядов максимальное число нулей.
Теорема (Теорема Лапласа)
Определитель равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:
|
|
(1.5.1) |
Формула (1.5.1) называется Разложением определителя по I–ой строке. Аналогичное утверждение имеет место и для Разложения по любому столбцу.
Определение
Квадратная матрица называется Вырожденной если ее определитель равен нулю.
Пример
Вычислить определитель матрицы A 4–го порядка:

По свойству 9 вычислим detA, разлагая его, например, по элементам 3–го столбца:
![]()
Преобразуем детерминант следующим образом: умножим 2–ю строку на 2 и прибавим к 3–й строке; умножим 2–ю строку на –6 и прибавим к 4–й строке. Получаем
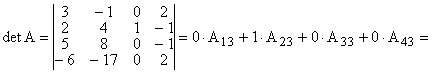

| < Предыдущая | Следующая > |
|---|