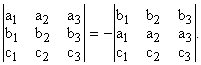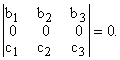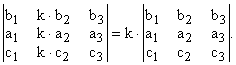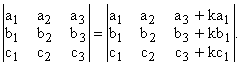Глава 04. Свойства определителей

Свойство 1

При транспонировании матрицы ее определитель не изменяется, т. е.:

DetA* = detA

(1.4.1)

Свойство 2

При перестановке двух параллельных рядов (строк либо столбцов) матрицы знак ее определителя изменяется на противоположный. Абсолютное значение определителя при этом не меняется.

(1.4.2)

Свойство 3

Определитель, содержащий два одинаковых ряда, равен нулю:

(1.4.3)

Свойство 4

Определитель, содержащий ряд из нулей, равен нулю:

(1.4.4)

Свойство 5

Общий множитель всех элементов одного ряда определителя можно вынести за знак определителя:

(1.4.5)

Свойство 6

Если все элементы какого–либо ряда определителя представлены в виде суммы двух слагаемых, то такой определитель можно представит в виде суммы двух определителей, у которого элементы рассматриваемого ряда равны соответствующим слагаемым. А остальные элементы у всех трех определителей одни и те же:

(1.4.6)

Свойство 7

Определитель не изменится, если к элементам какого–либо его ряда прибавить соответствующие элементы параллельного ему ряда, умноженного на одно и то же число:

(1.4.7)

Свойство 8

Определитель не изменится, если к элементам какого–либо ряда прибавить соответствующие элементы параллельного ему ряда, умноженные на одно и то же число.

(1.4.8)

Минором Mik элемента Aik определителя называется определитель, который получается из данного после вычеркивания I–ой строки и K–го столбца, на пересечении которых стоит этот элемент.

Пример

DetA=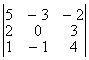. Найти миноры Mik.

Решение

Минор M11 элемента A11=5 равен:

Минор M32 элемента A32=–1 равен:

Алгебраическим дополнением Aik элемента Aik определителя называется минор этого элемента, взятый со знаком “+”, если I+K – четное число, и со знаком “–“, если I+K – нечетное число, т. е.

Aik =(–1)I+K Mik.

(1.4.9)

Пример

A11 = (–1)1+1 M11 = M11, A12 = (–1)1+2 M12 = – M12, A32 = (–1)3+2 M32 = – M32 и т. д.

Свойство 9

Определитель равен сумме произведений элементов какого–либо его ряда на их алгебраические дополнения, т. е. детерминант матрицы (1.3.3) равен

DetA = A11A11 + A12A12 + A13A13; DetA = A12A12 + A22A22 + A23A23 и т. д.

(1.4.10)

Пример

Вычислить определитель матрицы:

Решение

DetA = A11A11 + A12A12 + A13A13.

Итак, detA = 3×7 + (–2) ×(–10) + 0×(–5) = 41.

Свойство 10

Сумма произведений элементов какого–либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ему ряда равна нулю:

A11A21 + A12A22 + A13A13 = 0, A11A13 + A21A23 + A31A33 = 0 и т. д.

(1.4.11)

< Предыдущая		Следующая >