Глава 02. Действия над матрицами
1. Сложение матриц.
Пусть
|
|
(1.2.1) |
Суммой двух матриц A и B одинаковой размерности называется матрица C = A + B той же размерности, элементы которой равны сумме соответствующих элементов матриц A и B, т. е.
|
|
(1.2.2) |
Пример
![]() ,
, ![]() ,
, ![]() .
.
2. Умножение матрицы на число.
Произведением матрицы A на число l называется матрица C = lA, элементы которой равны элементам матрицы A, умноженным на число l, т. е.
|
|
(1.2.3) |
Матрица –A = (–1)×A называется противоположной матрице A. Очевидно, что A + (–A) = 0, где 0 – нулевая матрица той же размерности, что и матрица A.
Легко проверить, что операции сложения матриц и умножения матрицы на число, называющиеся линейными операциями, обладают следующими свойствами:
|
|
(1.2.4) |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
|
3. Вычитание матриц.
Разностью матриц A и B одинаковой размерности называется такая матрица C = A – B, сумма которой с матрицей B равна матрице A.
|
|
(1.2.5) |
Чтобы получить матрицу C = A – B, достаточно из элементов матрицы A вычесть соответствующие элементы матрицы B:
|
|
(1.2.7) |
4. Умножение матриц.
Произведением двух матриц A и B, заданных в указанном порядке, называется такая матрица С = A×B, каждый элемент которой Cik равен сумме произведений элементов I–ой строки матрицы A на соответствующие элементы K–го столбца матрицы B.
Матрицы A и B можно перемножить, если количество элементов в строке матрицы A равно количеству элементов в столбце матрицы B.
Пример
 ;
; ![]() . Найти A×B.
. Найти A×B.
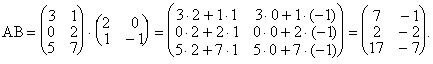
Замечание
Произведение матриц BA рассмотренных в приведенном выше примере, не существует, т. к. число столбцов (2) матрицы B (первого множителя) не равно числу строк (3) матрицы A (второго множителя).
Пример
![]()
![]() Найти A×B и B×A.
Найти A×B и B×A.
![]() ,
, ![]() .
.
Как видим из примера, A×B ¹ B×A, т. е. произведение матриц не обладает коммутативным свойством.
Свойства произведения матриц:
|
|
(1.2.8) |
|
| |
|
| |
|
| |
|
| |
|
|
| < Предыдущая | Следующая > |
|---|
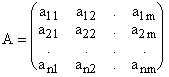 ;
;  .
.