Глава 01. Основные сведения о матрицах
Понятие матрицы и основанный на нем раздел математики – Матричная алгебра. Значительная часть математических моделей объектов и процессов записывается в достаточно простой и компактной матричной форме.
Определение
Матрицей Называется совокупность N×M чисел, расположенных в виде таблицы, содержащей N строк и M столбцов.
Общее обозначение
|
A= |
(1.1.1) |
Числа Aik (I = 1, 2, …, N; K = 1, 2, …, M), составляющие матрицу, называются ее Элементами. Первый индекс обозначает Номер строки, а второй – Номер столбца.
Если матрица имеет N строк и M столбцов, то говорят, что матрица имеет Размерность N´M.
Матрица, все элементы которой равны нулю, называется Нулевой.
Для матриц Одинаковой размерности устанавливается понятие их равенства: две матрицы Равны тогда и только тогда, когда Равны их соответствующие элементы.
Матрица, состоящая из одной строки, называется Матрицей (Вектором) – строкой, а из одного столбца – Матрицей (Вектором) – столбцом. Например,
![]() – матрица–строка,
– матрица–строка,
 – матрица–столбец.
– матрица–столбец.
Если N=M, то матрица называется Квадратной.
Квадратную матрицу, содержащую N строк и N столбцов, называют Матрицей n–го порядка.
Квадратная матрица, у которой равны нулю все элементы, кроме, может быть, элементов стоящих на главной диагонали, называется Диагональной.
Диагональная матрица, у которой все диагональные элементы равны единице, называется Единичной и обозначается E.
|
E= |
(1.1.2) |
Транспонированием матрицы A называется перемена местами строк и столбцов матрицы с сохранением их номеров. Полученная таким образом матрица называется Транспонированной и обозначается A*.
Пример
 ,
, ![]() .
.
Ясно, что (A*)* = A. Матрица, совпадающая со своей транспонированной (A* = A), называется Симметрической.
| Следующая > |
|---|
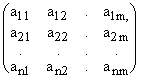 .
. .
.