Глава 10. Применение матриц для решения систем линейных уравнений
Используя обратную матрицу, можно решить систему линейных уравнений, у которой число уравнений равно числу неизвестных, если detA ¹ 0.
Обозначим:
|
|
(1.10.1) |
Где X – матрица неизвестных, B – матрица свободных членов.
При таких обозначениях систему линейных уравнений
|
|
(1.10.2) |
Можно записать в матричной форме:
|
|
(1.10.3) |
Умножим обе части полученного матричного уравнения Слева на A–1: ![]() .
.
Далее, используя свойства произведения матриц, получим: ![]()
![]()
|
|
(1.10.4) |
Итак, чтобы найти матрицу неизвестных, достаточно матрицу A–1, обратную матрице A, умножить на матрицу свободных членов.
Пример
Решить систему уравнений с помощью обратной матрицы:

Обозначим:
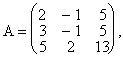
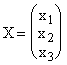 ,
,  .
.
Вычислим определитель основной матрицы системы: ![]() Так как detA¹0, систему можно решать матричным методом. Найдем матрицу A–1, обратную матрице A:
Так как detA¹0, систему можно решать матричным методом. Найдем матрицу A–1, обратную матрице A:  Вычислим алгебраические дополнения Aik (I, K = 1, 2, 3) к элементам Aik матрицы A: A11 = –23, A12 = –14, A13 = 11, A21 = 23, A22 = 1, A23 = –9, A31 = 0, A32 = 5, A33 = 1.
Вычислим алгебраические дополнения Aik (I, K = 1, 2, 3) к элементам Aik матрицы A: A11 = –23, A12 = –14, A13 = 11, A21 = 23, A22 = 1, A23 = –9, A31 = 0, A32 = 5, A33 = 1.
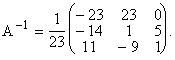
Проверим, верно ли найдена A–1:
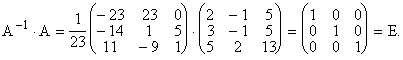
Матрица A–1 найдена верно. Находим матрицу неизвестных: ![]()

 Итак, X1 = –4, X2 = –2, X3 = 2. Проверим полученное решение: 2×(–4) – (–2) + 5×2 = –8 + 2 + 10 = 4, 3×(–4) – (–2) + 5×2 = –12 + 2 + 10 = 0, 5×(–4) + 2×(–2) + 13×2 = –20 – 4 + 26 = 2.
Итак, X1 = –4, X2 = –2, X3 = 2. Проверим полученное решение: 2×(–4) – (–2) + 5×2 = –8 + 2 + 10 = 4, 3×(–4) – (–2) + 5×2 = –12 + 2 + 10 = 0, 5×(–4) + 2×(–2) + 13×2 = –20 – 4 + 26 = 2.
| < Предыдущая | Следующая > |
|---|
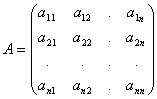 ,
,  ,
,  ,
,