Глава 11. Метод Гаусса
Метод Гаусса (или метод последовательного исключения неизвестных) состоит в том, что посредством последовательного исключения неизвестных данная система
|
|
(1.11.1) |
Превращается в ступенчатую (в частности, треугольную) систему
|
|
(1.11.2) |
Последняя система равносильна данной, но решать ее намного проще. Переход системы (1.11.1) к равносильной ей системе (1.11.2) называется Прямым ходом метода Гаусса, а нахождение переменных из системы (1.11.2) – Обратным ходом.
Рассмотрим этот метод на конкретных примерах.
Пример
Решить систему методом Гаусса:
Исключим x1 из 2–го т 3–го уравнений. Для этого 1–е уравнение умножим на (–2) и прибавим его ко 2–му, а затем 1–е уравнение умножим на (–3) и прибавим его к 3–му уравнению:
Новая система равносильна данной. Исключим из 3–го уравнения x2 для чего 2–е уравнение вычтем из 3–го:
Из последней системы находим x3 = –1, x2 = (56 + x3)/11 = (56 – 1)/11 = 55/11 = 5, x1 = –22 +4x2 – 3x3 = –22 + 4×5 – 3×(–1) = 1.
Пример
Решить систему методом Гаусса:
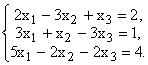
Умножим 2–е уравнение на (–2), а 1–е – на 3 и сложим, а затем 2–е уравнение умножим на (–5), а 3–е – на 3 и тоже сложим. Получим 
Исключим x2 из 3–го уравнения, умножив 2–е уравнение на (–2) и прибавив его к 3–му уравнению:
Последнее уравнение превратилось в неверное равенство. Это говорит о том, что система несовместна, т. е. решений не имеет.
Пример
Решить систему методом Гаусса:
Решение
Исключим x1 из 2–го и 3–го уравнений. Для этого умножим 1–е уравнение на (–1) и прибавляем его ко 2–му, далее умножим 1–е же на (–4) и прибавляем к 3–му уравнению:
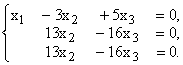
Так 2–е и 3–е уравнения одинаковы, одно из них отбрасываем:
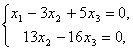
Число уравнений – два – меньше числа неизвестных – три. Такая система имеет бесчисленное множество решений. Пусть x3 = 13k, где k – произвольное число. Тогда x2 = (16/13)x3 = 16k, x1 = 3x2 – 5x3 = –17k.
Преобразования Гаусса удобно проводить не с самой системой уравнений, а с матрицей ее коэффициентов. Введем матрицу
|
|
(1.11.3) |
Называемую Расширенной матрицей системы (1.8.1) размера M´(N+1), так как матрица А дополнена столбцом свободных членов.
Пример
Найти решение системы уравнений методом Гаусса.
Решение
Составим расширенную матрицу этой системы, после чего выполним соответствующие шаги прямого хода Гаусса.
Шаг 1. Умножим первую строку матрицы AB на –2 и прибавим ее ко второй и третьей строке. Затем умножим первую строку матрицы AB на –3 и прибавим ее к четвертой строке. Получим
.
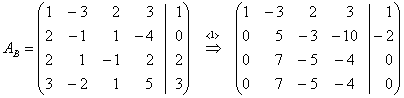Поскольку две последние строки являются линейно зависимыми, то одну из них можно отбросить.
Шаг 2. Умножим вторую строку полученной матрицы на –7/5 и прибавим ее к третьей строке. Получим
.
Заключительный вид расширенной матрицы соответствует совместной системе трех уравнений с четырьмя неизвестными, ранг которой меньше числа неизвестных. Полагая X4 свободной переменной, получаем
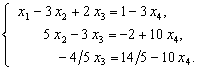
Из этой системы получаем обратным ходом метода Гаусса
.
Данная система уравнений имеет бесчисленное множество решений, так как X4 может принимать любые значения.
Отметим Достоинства метода Гаусса по сравнению с методом обратной матрицы и методом Крамера:
- метод является значительно Менее трудоемким;
- метод дает возможность однозначно Установить, совместна система или нет, а в случае
Совместности, найти ее решения;
- метод дает возможность Найти максимальное число линейно независимых уравнений, т. е. определить ранг матрицы системы.
| < Предыдущая | Следующая > |
|---|
