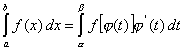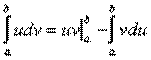Глава 81. Замена переменной и формула интегрирования по частям в определенном интеграле

Теорема

Пусть:

1) – непрерывная функция на отрезке ;

2) функция дифференцируема на , а непрерывна на ;

3) , .

Тогда справедлива формула

(7.13.1)

Формула (7.13.1) называется Формулой замены переменной или Подстановки в определенном интеграле.

Заметим, что при вычислении определенного интеграла с помощью замены переменной нет нужды возвращаться к прежней переменной, как при вычислении неопределенного интеграла, так как определенный интеграл представляет собой число, которое, согласно формуле (7.13.1) равно значению каждого из рассматриваемых интегралов. Теперь при подстановке следует сначала найти новые пределы интегрирования и выполнить необходимые преобразования подынтегральной функции.

Пример

1. .

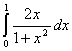Выполним подстановку . Тогда , при и при .

.

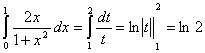2..

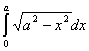Выполним подстановку .

Тогда , , , при , при . Подставляя все в исходный интеграл, получим

.

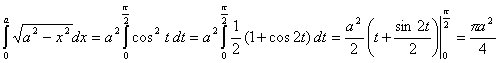Теорема: Пусть функции и имеют непрерывные производные на отрезке . Тогда справедлива формула

(7.13.2)

Равенство (7.13.2) называется Формулой интегрирования по частям в определенном интеграле.

Пример

1. .

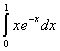Положим здесь , . Получаем

.

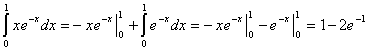2. .

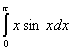Здесь , . Далее по формуле (7.13.2):

.

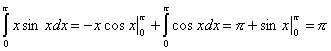< Предыдущая		Следующая >