Глава 82. Геометрические приложения определенных интегралов
C помощью определенного интеграла можно решать различные задачи в области физики, техники, геометрии, также в области экономики. Например, с помощью определенного интеграла вычисляются длины траекторий, движения, площади различных фигур, объемы тел и пр.
Вычисление площадей плоских фигур
Пусть функция 
неотрицательна и непрерывна на отрезке 
. Тогда по геометрическому смыслу определенного интеграла площадь S под кривой на численно равна определенному интегралу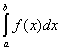 
, т. е. 
.
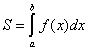Пример
Найти площадь фигуры, ограниченной линиями 
, 
, 
.
Из Рис. 7.14.1 видно, что площадь криволинейного треугольника ОАВ равна разности двух площадей: 
. Решая систему 
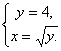, получаем координаты точки В (точки пересечения кривой и прямой ) В
. Тогда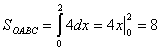 
, 
.
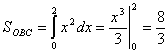Окончательно 
.
Отметим, что данная задача может быть решена другим способом.
По определению определенного интеграла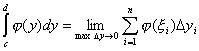 
.
Это равенство можно понимать так, что при построении интегральной суммы разбиению подвергается отрезок 
оси ординат. Соответственно точки 
– это ординаты, фиксированные на каждом из отрезков разбиения. Поэтому, если 
на , то интеграл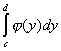 
численно равен площади криволинейной трапеции, ограниченной кривой 
и прямыми , 
, 
.
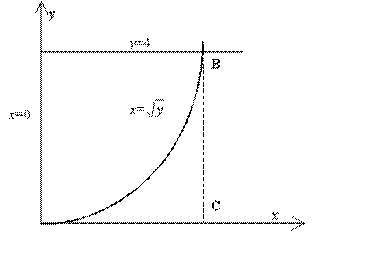
Рис. 7.14.1
Возвращаясь к нашей задаче, можно посчитать площадь следующим образом:
.
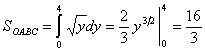Если функция Не положительна и непрерывна на отрезке 
, то площадь 
над кривой на отличается знаком от определенного интеграла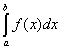 
:
.
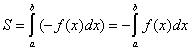Пример
Найти площадь фигуры, ограниченной линиями 
, 
, 
.
Из Рис. 7.14.2 видно, что искомая площадь криволинейного треугольника ОАВ может рассматриваться как площадь над кривой ОАВ на отрезке 
. Однако указанная кривая (ломаная)не задается одним уравнением. Поэтому для нахождения площади необходимо разбить треугольник ОАВ на две части 
. Координаты точек есть 
, 
и 
.
, 
.
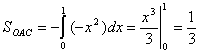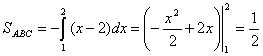Окончательно, 
.
Рис. 7.14.2
| < Предыдущая | Следующая > |
|---|
