Глава 80. Формула Ньютона–Лейбница

Согласно Теореме (см. раздел 7.10), непрерывная на отрезке функция имеет на этом отрезке первообразную, которая определяется формулой

,

(7.12.1)

Где С – произвольная постоянная. Подставляя в формулу (7.12.1), получаем с учетом свойства (1) определенного интеграла: 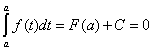, откуда .

Тогда из выражения (7.12.1) имеем .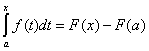

Полагая теперь , получаем формулу

.

(7.12.2)

Равенство (7.12.2) называется Основной формулой интегрального исчисления, или Формулой Ньютона–Лейбница.

Разность условно записывают символом . Формула (7.12.2) дает широкие возможности для вычисления определенных интегралов.

< Предыдущая		Следующая >
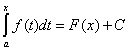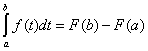