Глава 79. Определенный интеграл как функция верхнего предела

Если функция интегрируема на отрезке , то она интегрируема и на отрезке , где . Рассмотрим функцию аргумента

.

(7.10.1)

Назовем функцию Интегралом с переменным верхним пределом. В формуле (7.10.1) переменная интегрирования обозначена буквой , чтобы избежать путаницы с переменным верхним пределом .

Теорема

Непрерывная на отрезке функция имеет на этом отрезке Первообразную. Одной из первообразных является функция .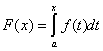

Таким образом, любая непрерывная на отрезке функция имеет на этом отрезке Первообразную в форме определенного интеграла с переменным верхним пределом. Поскольку всякая другая первообразная отличается от на постоянную величину, то связь между неопределенным и определенным интегралами имеет вид 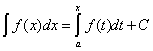, где С – произвольная постоянная.

< Предыдущая		Следующая >