Глава 78. Свойства определенного интеграла

Интеграл 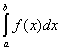был определен для случая, когда . Обобщим понятие определенного интеграла на другие случаи.

По определению полагаем 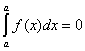как определенный интеграл от функции на отрезке нулевой длины.

1. .

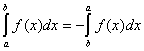Равенство (7.9.1) верно, поскольку при движении от к все длины частичных отрезков имеют отрицательный знак в частичной сумме (7.9.2).

2. Для любых чисел , и имеет место равенство

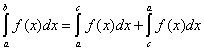
Постоянный множитель можно выносить за знак определенного интеграла

.

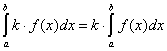Определенный интеграл от алгебраической суммы функций равен алгебраической сумме их определенных интегралов

.

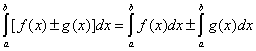3. .

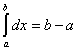Формулы оценки определенных интегралов

Будем полагать, что .

1. Если всюду на отрезке , то .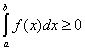

2. Если всюду на отрезке , то .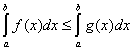

3. Если интегрируема на отрезке , то .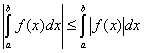

4. Если и – соответственно максимум и минимум функции на отрезке , то .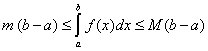

Теорема (о среднем)

Пусть функция интегрируема на отрезке и числа и – соответственно ее точная нижняя и точная верхняя грани на этом отрезке. Тогда

,

(7.10.1)

Где .

Примечание

Равенство (7.10.1) принимает особенно простой вид, если функция непрерывна на отрезке . Тогда числа и – соответственно наибольшее и наименьшее значения функции. По теореме о промежуточных значениях непрерывной функции на отрезке существует такая точка , то . Откуда

.

(7.10.2)

Рис. 7.10.1

Равенство (7.10.2) называется Формулой среднего значения, а величина – Средним значением функции на отрезке .

Формула (7.10.2) имеет ясный геометрический смысл (см. Рис. 7.10.1): при величина определенного интеграла равна площади прямоугольника высотой и основанием .

< Предыдущая		Следующая >
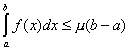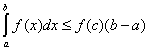