Глава 77. Понятие определенного интеграла

Пусть функция задана на отрезке . Разобьем отрезок на N произвольных частей точками

.

(7.9.1)

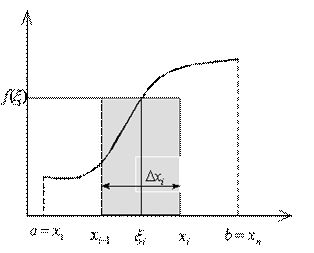
Рис. 7.9.1

Точки , разделяющие отрезок на Частичные отрезки длиной будем называть Точками разбиения. Выберем в каждом из частичных отрезков произвольную точку (см. Рис.7.9.1). Составим сумму произведений

.

(7.9.2)

Сумму (7.9.2) будем называть Интегральной суммой для функции на отрезке . Геометрический смысл величины показан на Рис. 7.9.1: это сумма прямоугольников с основаниями и высотами , . Введем еще одну величину: обозначим через l длину максимального частичного отрезка данного разбиения, т. е.

(7.9.3)

Определение

Конечный предел I интегральной суммы при , если он существует, называется Определенным интегралом от функции по отрезку :

.

(7.9.4)

Определенный интеграл обозначается символом .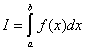

Если определенный интеграл (7.9.4) существует, то функция называется Интегрируемой на отрезке , числа и – соответственно нижним И верхним пределом интегрирования.

Вообще говоря, интегральная сумма (7.9.2) зависит от точек разбиения и промежуточных точек . Поскольку число тех и других стремится к бесконечности при , то определенный интеграл можно интерпретировать как бесконечную сумму бесконечно малых величин.

Теорема (Необходимое условие интегрируемости функции)

Интегрируемая на отрезке функция Ограничена на этом отрезке.

Заметим, что обратное утверждение не верно: ограниченная на отрезке функция может быть не интегрируемой на этом отрезке. Например, функция Дирихле

Не интегрируема на отрезке . Действительно, при любом разбиении этого отрезка можно выбрать рациональными точками и тогда интегральная сумма (7.9.2) ; если же взять иррациональными, то . Следовательно, не имеет предела при .

< Предыдущая		Следующая >