Глава 76. Интегрирование тригонометрических функций

Докажем интегрируемость в элементарных функциях любой функции вида

.

(7.8.1)

Докажем, что интеграл от этой функции рационализируется подстановкой

.

(7.8.2)

Действительно,

, , ,

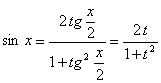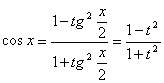Так что

.

(7.8.3)

Поскольку рациональная функция от рациональной функции представляет собой также рациональную функцию, то интеграл, стоящий в правой части последнего равенства, является интегралом от рациональной дроби. Подстановка называется Универсальной тригонометрической подстановкой.

Пример

Вычислить интеграл .

Решение

, , . .

Пример

Вычислить интеграл .

Решение

Используем подстановку (7.8.2).

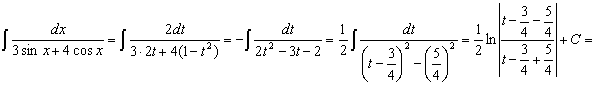
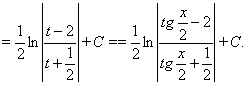
Рассмотрим некоторые Частные случаи, возникающие при интегрировании выражения

Если функция Нечетна относительно , т. е. , то применима подстановка . Тогда , а . Следовательно,

.

(7.8.4)

Если функция Нечетна относительно , т. е. , то применима подстановка . Тогда , а . Следовательно,

.

(7.8.5)

Наконец, если функция Четна Относительно и , т. е. , то применима подстановка . Тогда , , . Следовательно,

.

(7.8.6)

Пример

Вычислить интеграл .

Решение

.

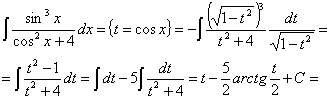
Пример

Вычислить интеграл .

Решение

.

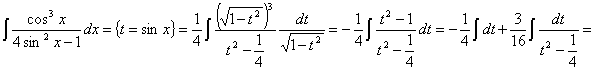
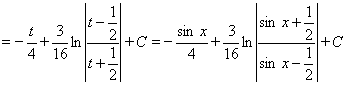Пример

Вычислить интеграл .

Решение

.

< Предыдущая		Следующая >
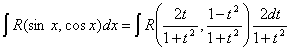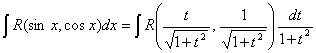