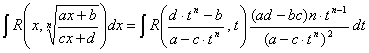Глава 75. Интегрирование некоторых видов иррациональностей

Докажем интегрируемость в элементарных функциях любой функции вида

,

(7.7.1)

Где – некоторые постоянные, – любое целое положительное число. Функцию такого вида мы будем называть Дробно–линейной иррациональностью.

Докажем, что интеграл от функции (7.7.1) при рационализируется подстановкой . В самом деле,, , ,

Так что

(7.7.2)

Поскольку рациональная функция от рациональной функции представляет собой также рациональную функцию, то интеграл, стоящий в правой части последнего равенства является интегралом от рациональной дроби. Тем самым Доказано, что интеграл от дробно–линейной иррациональной функции (7.7.1) Рационализируется подстановкой .

Пример

Вычислить интеграл .

Решение

Выполним подстановку . Тогда , .

.

Пример

Вычислить интеграл .

Решение

Применим подстановку . Тогда , , .

.

< Предыдущая		Следующая >
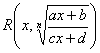