Глава 71. Интегралы от основных элементарных функций
Ранее мы получили основные производные элементарных функций. Приводимые ниже неопределенные интегралы представляют собой вычислительный аппарат интегрального исчисления. Часть формул непосредственно следует из определения интегрирования как операции, обратной дифференцированию. Справедливость всех формул легко проверить дифференцированием.
|
(7.3.1) |
Приведенные выше интегралы принято называть Табличными. Как было установлено ранее, операция дифференцирования не выводит функцию из класса элементарных. С операцией интегрирования дело обстоит иначе: интегралы от некоторых элементарных функций уже не являются элементарными функциями. Например:
![]() – интеграл Пуассона.
– интеграл Пуассона.
![]() или
или ![]() – интеграл Френеля.
– интеграл Френеля.
![]() – интегральный синус.
– интегральный синус.
![]() – интегральный косинус.
– интегральный косинус.
Каждый из этих интегралов есть функция, которая не является элементарной. Они играют большую роль в прикладных науках. Например, интеграл Пуассона является одним из основных в теории вероятностей и статистике.
Отметим несколько Полезных правил для вычисления интегралов.
Если известна первообразная функции ![]() , т. е.
, т. е. ![]() , а числа
, а числа ![]() и
и ![]() константы, то:
константы, то:
|
1. 2. 3. |
(7.3.2) |
Пример
Вычислим интегралы.
![]() ,
,
![]() ,
,
![]() ,
,
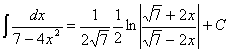 .
.
| < Предыдущая | Следующая > |
|---|