Глава 66. Производная по направления. Градиент

Пусть функция двух переменных задана в некоторой окрестности точки . Рассмотрим некоторое направление, определяемое единичным вектором , где . На прямой, проходящей по этому направлению через точку М, возьмем точку ,так что длина отрезка равна . Приращение функции определяется формулой: , где и связаны соотношениями и .

Рис. 6.5.1

Определение

Предел отношения при называется Производной функции по направлению и обозначается символом :

Если функция дифференцируема в точке , то ее приращение в этой точке, с учетом соотношений для и , может быть записана в форме

Поделив обе части этого равенства на и переходя к пределу при , получаем формулу для производной функции по направлению:

.

(6.5.1)

Рассмотрим функцию трех переменных , дифференцируемую в точке .

Определение

Градиентом функции в точке М называется Вектор, координаты которого равны соответственно частным производным в этой точке.

Для обозначения градиента функции используется обозначение grad u:

Grad u = .

(6.5.2)

Поскольку единичный вектор имеет координаты , то производная по направлению для случая функции трех переменных запишется в виде

Grad U,

(6.5.3)

Т. е. имеет форму Скалярного произведения векторов и grad U.

Таким образом, Градиент функции характеризует Направление и Величину максимальной скорости возрастания этой функции в точке.

< Предыдущая		Следующая >
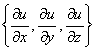