Глава 58. Выпуклость функции. Точки перегиба
Ранее мы подробно изучали точки экстремума, нахождение которых во многом определяет структуру графика функции. Определим теперь другие «узловые» точки функции, которые также следует найти, чтобы качественно построить ее график.
Определение
Функция ![]() называется Выпуклой вниз (Вверх) на
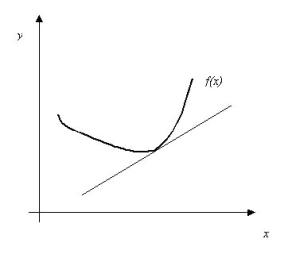
называется Выпуклой вниз (Вверх) на ![]() , если ее график расположен не ниже (не выше) любой ее касательной на этом интервале (рис. 5.10.1).
, если ее график расположен не ниже (не выше) любой ее касательной на этом интервале (рис. 5.10.1).
Теорема
Функция Выпукла вниз (вверх) на промежутке X тогда и только тогда когда ее Первая производная на этом промежутке монотонно Возрастает (убывает).
Теорема
Если функция ![]() имеет на интервале
имеет на интервале ![]() вторую производную и
вторую производную и ![]() то график функции имеет на
то график функции имеет на ![]() Выпуклость, направленную вниз (вверх) (Рис. 5.10.2).
Выпуклость, направленную вниз (вверх) (Рис. 5.10.2).
Определение
Точкой перегиба графика непрерывной функции называется точка, разделяющая интервалы, в которых функция выпукла вверх и вниз.
|
Рис. 5.10.1 |
Рис.5.10.2. |
Теорема (Необходимое условие точки перегиба)
Вторая производная ![]() дважды дифференцируемой функции в точке перегиба
дважды дифференцируемой функции в точке перегиба ![]() Равна нулю, т. е.
Равна нулю, т. е. ![]() .
.
Отметим, что условие ![]() не всегда означает наличие точки перегиба, например, график функции
не всегда означает наличие точки перегиба, например, график функции ![]() не имеет перегиба в точке
не имеет перегиба в точке ![]() , хотя вторая производная равна нулю. Поэтому равенство нулю второй производной является необходимым. Точки, в которых вторая производная равна нулю или не существует будем называть Критическими. В каждой такой точке необходимо исследовать дополнительно вопрос о существовании точки перегиба.
, хотя вторая производная равна нулю. Поэтому равенство нулю второй производной является необходимым. Точки, в которых вторая производная равна нулю или не существует будем называть Критическими. В каждой такой точке необходимо исследовать дополнительно вопрос о существовании точки перегиба.
Теорема (Достаточное условие точки перегиба)
Если Вторая производная ![]() дважды дифференцируемой функции при переходе через некоторую точку
дважды дифференцируемой функции при переходе через некоторую точку ![]() Меняет свой знак, то
Меняет свой знак, то ![]() есть Точка перегиба ее графика.
есть Точка перегиба ее графика.
Следует отметить, что если критическая точка дифференцируемой функции не является точкой экстремума, то она является точкой перегиба.
Схема исследования функции на выпуклость и точки перегиба
1. Найти вторую производную функции ![]() .
.
2. Найти точки, в которых вторая производная ![]() или не существует.
или не существует.
3. Исследовать знак второй производной слева и справа от найденных точек и сделать вывод об интервалах выпуклости и наличии точек перегиба.
4. Найти значения функции в точках перегиба.
| < Предыдущая | Следующая > |
|---|