Глава 57. Экстремум функции

Определение

Точка называется точкой Локального максимума (Минимума) функции , Если для любого числа в некоторой окрестности точки выполнено неравенство .

Термины «локальный минимум» и «локальный максимум» объединены общим названием «Локальный экстремум».

Теорема

(Необходимое условие существования локального экстремума). Для того чтобы функция имела экстремум в точке , необходимо, чтобы ее Производная в этой точке равнялась нулю или не существовала.

Геометрический смысл теоремы заключается в следующем: если в точках локальных экстремумов существуют касательные, то они параллельны оси .

Точки, в которых выполнено необходимое условие экстремума называют Критическими или Стационарными (а также Точками возможного экстремума). Очевидно, что эти точки должны входить в ОДЗ функции. Таким образом, если в какой–либо точке имеется экстремум, то эта точка критическая, однако обратное утверждение неверно: критическая точка вовсе не обязана быть точкой экстремума.

Это можно показать на примерах функций . Для первой функции точка является точкой экстремума, а для второй – нет.

Сформулируем достаточные условия существования локального экстремума.

Теорема (Первое достаточное условие экстремума)

Пусть функция Дифференцируема в некоторой окрестности точки . Если при переходе через точку слева направо производная Меняет знак с плюса на минус, то в точке функция имеет Локальный максимум, а если с Минуса на плюс, то – точка Минимума. Если же не меняет знака в Окрестности точки , то данная функция Не имеет локального экстремума в этой точке.

Геометрический смысл теоремы иллюстрирует Рис. 5.9.1.

Отметим также, что дифференцируемость в самой точке Вовсе не обязательна. Например, функция имеет экстремум (минимум) в точке , но не дифференцируема в ней.

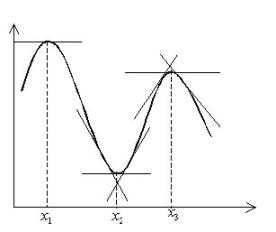
Рис. 5.9.1

Схема исследования функции на локальный экстремум

1. Найти производную .

2. Найти критические точки функции, в которых производная или не существует.

3. Исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии экстремумов функции.

4. Найти экстремумы функции.

Пример

Исследовать на экстремум функцию .

Решение

Найдем производную и приравняем нулю:.

Нули производной: . Исследуем знаки первой производной.

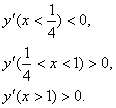
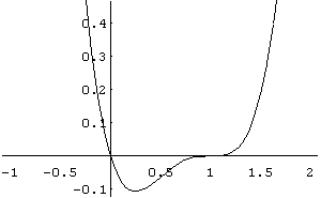
Так как при переходе через точку производная меняет знак с минуса на плюс, то точка является точкой минимума. При переходе через точку производная знак не меняет, поэтому точка не является точкой экстремума.

Теорема (Второе достаточное условие экстремума)

Если первая производная дважды дифференцируемой функции Равна нулю в некоторой точке , а Вторая производная в этой точке положительна , то точка есть Точка минимума функции ; если Вторая производная отрицательна – , то – точка Максимума.

Второе достаточное условие экстремума утверждает, что если в критической точке , то в этой точке имеется экстремум. Обратное утверждение неверно – экстремум в критической точке может быть и при равенстве нулю в ней второй производной, например, для функции и критической точки .

При решении прикладных задач, в частности оптимизационных, важное значение имеют задачи на нахождение наибольшего и наименьшего значений (глобального максимума и глобального минимума) функции на промежутке .

Ранее отмечалось, что если функция непрерывна на отрезке , то она принимает на нем наибольшее и наименьшее значения. Наибольшее или наименьшее значения функции могут достигаться как в точках экстремума, так и на концах отрезка.

Для отыскания наибольшего и наименьшего значений на отрезке рекомендуется пользоваться следующей схемой:

1. Найти производную .

2. Найти критические точки функции, в которых или не существует.

3. Найти значения функции в критических точках и на концах отрезка и выбрать из них наибольшее и наименьшее.

< Предыдущая		Следующая >