Глава 46. Замечательные пределы

Первый замечательный предел

Теорема

Предел функции в точке существует и равен Единице, т. е.

(4.6.1)

Предел (4.6.1) называется первым замечательным пределом и применяется при вычислении ряда других пределов. Рассмотрим несколько примеров на применение предела (4.6.1).

Пример

Найти предел функции При .

Решение

Преобразуем данную дробь так, чтобы в знаменателе был аргумент синуса; только тогда можно будет применить первый замечательный предел, поскольку при пределом также является нуль:

 Пример

Найти .

Решение

Первый замечательный предел здесь непосредственно применить нельзя, так как при знаменатель дроби стремится к нулю. Для решения задачи необходимо преобразовать данную дробь:

 Второй замечательный предел

Теорема

Предел функции при существует и равен , т. е.

.

(4.6.2)

Предел (4.6.2) называется вторым замечательным пределом и применяется при вычислении ряда других пределов. E = 2.718281…

Пример

Найти .

Решение

Выполним здесь замену переменной, полагая . Тогда при , т. е.

Пример

Найти

Решение

Преобразуем дробь под знаком предела:

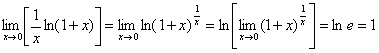
Пример

Найти .

Решение

Сделаем замену . Тогда

Пример

Найти .

Решение

Сделаем замену . Тогда

< Предыдущая		Следующая >