Глава 35. Гиперболоиды
Определение
Гиперболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются Каноническими уравнениями вида
|
|
(2.21.1) |
|
|
(2.21.2) |
|
|
|
|
Рис. 2.21.1 |
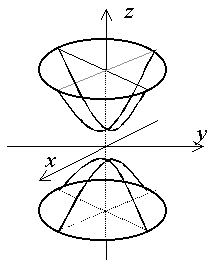
Рис. 2.21.2 |
Гиперболоид, определяемый уравнением (2.21.1) называется Однополостным (Рис. 2.21.1); гиперболоид, определяемый уравнением (2.21.2), – Двуполостным (Рис. 2.21.2). Величины ![]() называются Полуосями гиперболоида. Центр симметрии в уравнениях (2.26.1) и (2.26.2) совпадает с началом координат.
называются Полуосями гиперболоида. Центр симметрии в уравнениях (2.26.1) и (2.26.2) совпадает с началом координат.
Ось ![]() является осью Однополостного гиперболоида. Горизонтальные плоскости
является осью Однополостного гиперболоида. Горизонтальные плоскости ![]() пересекают однополостный гиперболоид (Рис. 2.21.1) по эллипсам, причем наименьший (“горловой”) эллипс получается при
пересекают однополостный гиперболоид (Рис. 2.21.1) по эллипсам, причем наименьший (“горловой”) эллипс получается при ![]() и определяется уравнением
и определяется уравнением ![]() . Вертикальные плоскости пересекают однополостный гиперболоид по гиперболам (Рис. 2.21.1). Гиперболоид, у которого полуоси
. Вертикальные плоскости пересекают однополостный гиперболоид по гиперболам (Рис. 2.21.1). Гиперболоид, у которого полуоси ![]() и
и ![]() равны, является Поверхностью вращения Гиперболы вокруг оси
равны, является Поверхностью вращения Гиперболы вокруг оси ![]() .
.
Если центр перенести в точку ![]() , то каноническое уравнение однополостного гиперболоида принимает вид
, то каноническое уравнение однополостного гиперболоида принимает вид
|
|
(2.21.3) |
Поверхность Двуполостного гиперболоида имеет две вершины в точках (![]() ) расположенных на оси
) расположенных на оси ![]() (Рис. 2.21.2). Горизонтальные плоскости
(Рис. 2.21.2). Горизонтальные плоскости ![]() пересекают поверхность двуполостного гиперболоида по эллипсам, вертикальные – по гиперболам. Гиперболоид, у которого полуоси
пересекают поверхность двуполостного гиперболоида по эллипсам, вертикальные – по гиперболам. Гиперболоид, у которого полуоси ![]() и
и ![]() равны, является Поверхностью вращения гиперболы вокруг оси
равны, является Поверхностью вращения гиперболы вокруг оси ![]() .
.
Каноническое уравнение двуполостного гиперболоида со смещенным центром имеет вид
|
|
(2.21.4) |
| < Предыдущая | Следующая > |
|---|