Глава 36. Параболоиды

Определение

Параболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями

,	(2.22.1)
,	(2.22.2)

Где и – положительные числа, называемые Параметрами параболы. 

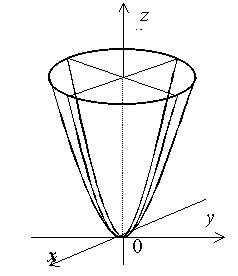
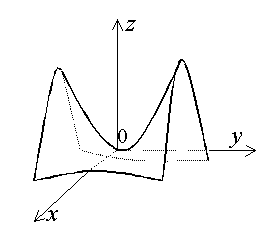
Параболоид, определяемый уравнением (2.22.1), называется Эллиптическим (Рис. 2.22.1); параболоид, определяемый уравнением (2.22.2), называется Гиперболическим (Рис. 2.22.2). Уравнения (2.22.1) и (2.22.2) называют Каноническими уравнениями соответствующих параболоидов.

Осью Эллиптического параболоида Является кОординатная ось . Его вершина находится в начале координат. Горизонтальные плоскости пересекают поверхность эллиптического параболоида по эллипсам, вертикальные – по параболам. В случае, когда , параболоид, определяемый уравнением (2.22.1), является поверхностью вращения (вокруг оси ). Каноническое уравнение эллиптического параболоида со смещенным центром имеет вид

.

(2.22.3)

Рис. 2.22.1	Рис. 2.22.2

Ось гиперболического параболоида совпадает с осью . Горизонтальные плоскости пересекают поверхность параболоида по гиперболам, причем гиперболы, полученные при , сопряжены с гиперболами, полученными при . Вертикальные плоскости пересекают поверхность параболоида по параболам.

< Предыдущая		Следующая >