Глава 27. Гипербола, ее эксцентриситет, директриса и асимптоты
Определение
Гиперболой называется геометрическое место точек плоскости, для каждой из которых абсолютное значение разности расстояний до двух данных точек плоскости 
и 
, называемых фокусами, есть величина постоянная, равная 
.
Расстояние между фокусами – 
.
Если оси декартовой прямоугольной системы координат выбраны так, что фокусы данной гиперболы располагаются на оси абсцисс симметрично относительно начала координат (рис. 2.13.1), то каноническое уравнение гиперболы имеет вид
|
|
(2.13.1) |
Где 
. Уравнение вида (2.13.1) называется Каноническим Уравнением гиперболы. При указанном выборе системы координат оси координат являются Осями симметрии гиперболы, а начало координат – ее Центром симметрии. Ось 
называется Действительной осью, а 
– Мнимой осью гиперболы. Точки пересечения гиперболы с осью называются Вершинами гиперболы.
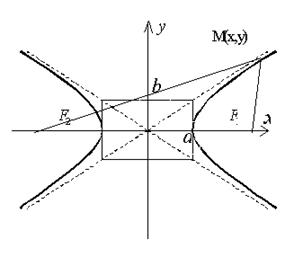
Рис. 2.13.1.
Прямоугольник со сторонами и 
, расположенный симметрично относительно осей гиперболы и касающийся ее в вершинах, называется основным прямоугольником гиперболы. Диагонали основного прямоугольника (неограниченно продолженные) являются асимптотами гиперболы и определяются уравнениями
|
|
(2.13.2) |
, 
.Эксцентриситетом гиперболы (как и эллипса) называется число 
, где 
– расстояние от центра гиперболы до ее вершины. Очевидно, что для любой гиперболы 
.
Если 
– произвольная точка гиперболы, то отрезки 
и 
называются Фокальными радиусами точки М. Фокальные радиусы правой ветви гиперболы могут быть вычислены по формулам 
и 
. Фокальные радиусы левой ветви гиперболы – по формулам 
и 
.
Если гипербола задана уравнением (2.13.1), то прямые, определяемые уравнениями 
, называются ее Директрисами.
Пример
Составить уравнение гиперболы, фокусы которой лежат на оси абсцисс, симметрично относительно начала координат, если точка 
лежит на гиперболе и известны уравнения асимптот 
.
Из уравнений для асимптот находим 
, или 
. Поскольку точка 
принадлежит гиперболе, ее координаты удовлетворяют уравнению (2.13.1): 
, где 
или 
. Отсюда находим 
, тогда 
, следовательно, уравнение гиперболы имеет вид 
.
Пример
Дана гипербола 
. Найти ее полуоси и 
, фокусы, эксцентриситет, уравнения асимптот.
Разделим обе части этого уравнения на 144. Получим 
. Значит 
, следовательно оси гиперболы соответственно равны 
и 
. Так как 
, то фокусы гиперболы находятся в точках 
и 
. Эксцентриситет гиперболы вычисляется по формуле 
. В соответствии с (2.13.2), уравнения асимптот имеют вид: 
.
| < Предыдущая | Следующая > |
|---|
