Глава 25. Окружность

Определение

Окружностью называется геометрическое место точек плоскости, равноудаленных от ее центра.

Пусть точка – Центр окружности. Расстояние любой точки окружности до центра обозначим через – Радиус окружности (Рис. 2.11.1). Пусть текущая точка окружности. Из определения окружности следует, что расстояние от точки до центра окружности будет равно радиусу этой окружности. Используя формулу для расстояния между двумя точками, получим каноническое уравнение окружности

.

(2.11.1)

Этому уравнению будут удовлетворять координаты точек, лежащих на окружности. Уравнение (2.11.1) называется Нормальным уравнением окружности.

Если центр окружности лежит в начале координат, то есть , то уравнение (2.11.1) принимает вид:

(2.11.2)

Этот простейший вид уравнения окружности называется Каноническим.

Рис. 2.11.1.

Пример

Составить уравнение окружности, проходящей через точку , если центр окружности совпадает с точкой .

Решение

Поскольку окружность проходит через точку , координаты этой точки удовлетворяют уравнению , то есть , откуда , тогда уравнение окружности принимает вид .

Пример

Найти те касательные к окружности , которые параллельны прямой .

Решение

Искомые прямые параллельны данной прямой и перпендикулярны диаметру данной окружности в точках касания. Составим уравнение диаметра: (центр окружности совпадает с началом координат). Учитывая, что диаметр и данная прямая перпендикулярны. Находим угловой коэффициент диаметра. Он равен . Тогда уравнение диаметра имеет вид . Для того, чтобы составить уравнение касательных, необходимо найти координаты точек касания. Решив совместно систему уравнений 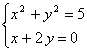, находим две точки касания, лежащие на противоположных концах диаметра: , . Угловой коэффициент искомых касательных равен . Тогда с помощью уравнения прямой, проходящей через заданную точку с заданным угловым коэффициентом можно найти уравнения касательных: и .

< Предыдущая		Следующая >