Глава 20. Уравнение прямой с угловым коэффициентом. Уравнение прямой в отрезках

Рассмотрим общее уравнение прямой (2.5.1). Если В0, то разрешив его относительно У И обозначив , получим уравнение прямой с угловым коэффициентом:

(2.6.1)

 

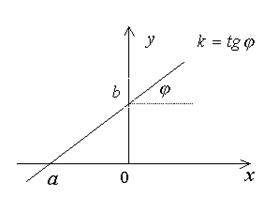
Рис. 2.6.1

Здесь , где – угол наклона, образуемый прямой (2.5.1) и положительным направлением оси Ox, B – ордината точки пересечения прямой с осью ОY (Рис. 2.6.1).

Если в общем уравнении прямой (2.5.1) коэффициент , и , то разделив его на , получим . Обозначив , приходим к Уравнению прямой в отрезках:

.

(2.6.2)

В этом уравнении числа и соответственно равны абсциссе и ординате точек пересечения прямой с осями ОX и ОY (Рис. 2.6.1).

Пример

Из общего уравнения прямой (2.1.1) получить:

А) уравнение прямой с угловым коэффициентом (2.6.1);

Б) уравнение прямой в отрезках (2.6.2).

Решение

Выражая Y из данного уравнения, получим: , где , . Разделив общее уравнение на –6, получим: .

< Предыдущая		Следующая >