Глава 18. Смешанное произведение векторов. Условие компланарности трех векторов
Определение
Смешанным произведением трех векторов A, B и C Называется произведение, составленное следующим образом: ([A,B]×C), т. е. два вектора A и B умножаются векторно, а затем полученный вектор [A,B] скалярно умножается на третий вектор C. Смешанное произведение – это Число.
Если известны координаты перемножаемых векторов A = {ax, ay, az}, B = {bx, by, bz}, C = {cx, cy, cz}, то их смешанное произведение можно вычислить по формуле:
|
([A,B]×C) = |
(2.4.1) |
С геометрической точки зрения смешанное произведение векторов A, B И C с точностью до знака равно объему параллелепипеда, построенного на этих векторах, как на ребрах (рис. 2.4.1).

Рис. 2.4.1
Пример
Вычислить объем треугольной пирамиды, построенной на векторах A = {1, –1, 3}, B = {–2, 2, 1}и C = {3, –2, 5}.
Вычислим смешанное произведение векторов:
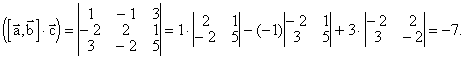
![]() (ед.3).
(ед.3).
Пример
Выяснить, лежат ли точки A(1,2,–1), B(0,1,5), C(–1,2,1) и D(2,1,3) в одной плоскости.
Очевидно, точки A, B и C лежат в одной плоскости, если векторы ![]() ,
, ![]() и
и ![]() компланарны.
компланарны.
Условием Компланарности трех векторов является Равенство нулю их смешанного произведения.
Найдем компоненты векторов:![]() = {0–1, 1–2, 5–(–1)} = {–1, –1, 6};
= {0–1, 1–2, 5–(–1)} = {–1, –1, 6};![]() = {–1–1, 2–2, 1–(–1)} = {–2, 0, 2};
= {–1–1, 2–2, 1–(–1)} = {–2, 0, 2};
![]() = {2–1, 1–2, 3–(–1)} = {1, –, 4}. Вычислим смешанное произведение:
= {2–1, 1–2, 3–(–1)} = {1, –, 4}. Вычислим смешанное произведение:
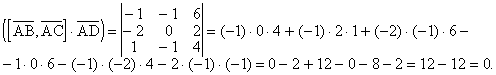
Так как смешанное произведение равно нулю, то вектора компланарны, а значит точки A, B, C и D лежат в одной плоскости.
| < Предыдущая | Следующая > |
|---|
