Глава 17. Векторное произведение векторов. Условие коллинеарности двух векторов

Определение

Векторным произведением вектора A на вектор B называется вектор C, который определяется следующим образом:

1. Длина вектора C равна произведению длин перемножаемых векторов на синус угла между ними:

.

(2.3.1)

2. Вектор C перпендикулярен обоим перемножаемым векторам:

.

(2.3.2)

3. Направление вектора c таково, что, если смотреть из его конца вдоль вектора, то поворот на наименьший угол от первого сомножителя A ко второму сомножителю B виден совершающимся против движения часовой стрелки (рис. 2.3.1).

Рис. 2.3.1

Обозначается векторное произведение так: [Ab], [A, b] или A´B. Если известны координаты перемножаемых векторов, т. е. A = {ax, ay, az}, B = {bx, by, bz}, то их векторное произведение можно найти по формуле:

(2.3.3)

Пример

Найти векторное произведение векторов A = {3, 3, 2}, B = {5, –2, 9}.

Решение

Основные свойства векторного произведения:

1. [A, b] = – [B, a].

2. [A,(B + c)] = [A,B] + [A,C].

3. l[A,B] = [(lA),B] = [A,(lB)].

4.

5. [A,A] = 0.

Пример

Даны вершины треугольника A(1,2,0), B(3,0,–3), C(5,2,6). Вычислить его площадь.

Решение:

Треугольник ABC можно рассматривать построенным на векторах и (рис. 2.3.2).

Рис. 2.3.2

Найдем координаты векторов  и . = {3–1, 0–2, –3–0} = {2, –2, –3};

= {5–1, 2–2, 6–0} = {4, 0, 6}. Вычислим векторное произведение этих векторов:

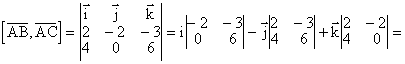
Находим длину вектора :

Пример

Сила F = {2, –4, 5} приложена к точке A(4,–2,3). Найти момент этой силы относительно точки O(3,2,–1)

Решение

По определению момент силы есть M0 = F ´ AO. AO = {3–4, 2–(–2), –1–3} = {–1, 4, –4}.

M0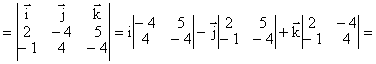

< Предыдущая		Следующая >