Глава 16. Скалярное произведение векторов. Условие ортогональности двух векторов
Определение
Скалярным произведением векторов A и B называется число, равное произведению длин этих векторов на косинус угла 
между ними. Обозначается скалярное произведение так: (Ab), (A, b) или A×B. Итак
|
|
(2.2.1) |
Поскольку 
(см. рис. 2.2.1), то получаем:
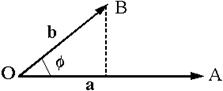
Рис. 2.2.1
|
|
(2.2.2) |
, 
.Если известны координаты перемножаемых векторов, т. е. A={ax, ay, az}, B={bx, by, bz}, то скалярное произведение этих векторов можно вычислить по формуле:
|
A×B = axbx + ayby + azbz. |
(2.2.3) |
Свойства скалярного произведения:
1. A×B = B×A.
2. A×(B + c) = A×B + A×C.
3. l( a×B) = (lA)×B = A×(lB).
4. Векторы A И B взаимно перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю:
|
|
(2.2.4) |
.5. Скалярный квадрат вектора равен квадрату его длины:
|
|
(2.2.5) |
.Пример
Даны вершины треугольника A(–1,–2,4), B(–4,–2,0), C(3,–2,1). Определить его внутренний угол при вершине B.
Внутренний угол при вершине B (рис. 2.2.2) – это угол между векторами 
и 
: 
.
Рис. 2.2.2
Найдем координаты векторов и : = {xA–xB, yA–yB, zA–zB} = {3, 0, 4}; = {xC–xB, yC–yB, zC–zB} = {7, 0, 1}. Скалярное произведение этих векторов и их длины:
.
Итак
.
Пример
Даны три вектора: A = 3I – 6J – K, B = I +4J – 5K, C = 3I – 4J + 12K. Найти 
.
Векторы заданы их разложением по базису. Выпишем их координаты: A = {3, –6, –1}, B = {1, 4, –5}, C = {3, –4, 12}, A + B = {3+1, –6+4, –1+(–5)} = {4, –2, 6}.
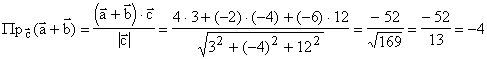
Знак “минус” говорит о том, что угол между векторами A + B и C Тупой.
Пример
Определить при каком значении m векторы A = mI – 3J + 2K и B = I + 2J – mK взаимно перпендикулярны.
Решение
A = {m, –3, 2}, B = {1, 2, –m}. Векторы взаимно перпендикулярны, если их скалярное произведение равно нулю: A×B = m – 6 – 2m = –6 – m; –6 – m = 0; m = –6.
| < Предыдущая | Следующая > |
|---|
